Question

【題目】綜合與實踐﹣四邊形旋轉中的數學

“智慧”數學小組在課外數學活動中研究了一個問題，請幫他們解答．

任務一：如圖1，在矩形ABCD中，AB=6，AD=8，E，F分別為AB，AD邊的中點，四邊形AEGF為矩形，連接CG．

（1）請直接寫出CG的長是______．

（2）如圖2，當矩形AEGF繞點A旋轉（比如順時針旋轉）至點G落在邊AB上時，請計算DF與CG的長，通過計算，試猜想DF與CG之間的數量關系．

（3）當矩形AEGF繞點A旋轉至如圖3的位置時，（2）中DF與CG之間的數量關系是否還成立？請說明理由．

任務二：“智慧”數學小組對圖形的旋轉進行了拓展研究，如圖4，在ABCD中，∠B=60°，AB=6，AD=8，E，F分別為AB，AD邊的中點，四邊形AEGF為平行四邊形，連接CG．“智慧”數學小組發現DF與CG仍然存在著特定的數量關系．

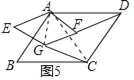
（4）如圖5，當AEGF繞點A旋轉（比如順時針旋轉），其他條件不變時，“智慧”數學小組發現DF與CG仍然存在著這一特定的數量關系．請你直接寫出這個特定的數量關系．

Answer 1

【答案】5

【解析】

（1）如圖1中，由此EG交CD于H，則四邊形FGHD是矩形．在Rt△CGH中，利用勾股定理即可解決問題；

（2）如圖2中，作FP⊥AD于P．利用勾股定理相似三角形的性質，分別求出CG、DF即可解決問題；

（3）成立．連接AG、AC．只要證明△ADF∽△ACG，可得 即可解決問題；

（4）在圖4中，通過計算即可解決問題；

（1）如圖1中，由此EG交CD于H，則四邊形FGHD是矩形．

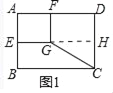
在Rt△CGH中，GH=DF=4，CH=DH=AE=3，

∴CG= =5．

故答案為：5．

（2）如圖2中，作FP⊥AD于P．

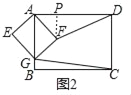
在矩形AEGF中，∵AE=3，EG=4，

∴AG=5，BG=AB-AG=1，

在Rt△CBG中，CG= ，

由△APF∽△AEG，可得 ，

∴ ，

∴AP= ，PF= ，DP=AD﹣AP=8﹣，

在Rt△PDF中，DF= ，

∴DF=CG．

（3）成立．理由如下：連接AG、AC．

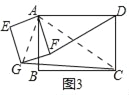
由旋轉可知：∠DAF=∠CAG，

由勾股定理可知：AC=，AG=5，

∵ ，，

∴，

∴△ADF∽△ACG，

∴，

∴DF=CG．

（4）如圖4中，延長EG交CD于H，作CK⊥GH于K．

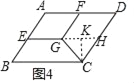
由題意可知四邊形FGHD是平行四邊形，四邊形AEGF是平行四邊形，

∴DF=GH=4，DH=FG=AE=3，CH=3，∠CHG=∠D=60°，

在Rt△CHK中，HK=，CK=，GK=GH﹣KH=，

在Rt△CGK中，CG= ，

∴CG=DF．

在圖5中，連接AG、AC．

同法可證：△ACG∽△ADF，可得：=，可得CG=DF．