
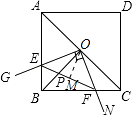
【題目】如圖,在正方形ABCD中,點O為對角線AC的中點,過點o作射線OG、ON分別交AB,BC于點E,F,且∠EOF=90°,BO、EF交于點P.則下列結論中:
⑴圖形中全等的三角形只有兩對;
⑵正方形ABCD的面積等于四邊形OEBF面積的4倍;
⑶BE+BF= ![]() OA;
OA;
⑷AE2+CF2=2OPOB.
正確的結論有( )個.
A.1
B.2
C.3
D.4
【答案】C
【解析】解:⑴錯誤.△ABC≌△ADC,△AOB≌△COB,△AOE≌△BOF,△BOE≌△COF;
⑵正確.∵△AOE≌△BOF,∴四邊形BEOF的面積=△ABO的面積= ![]() 正方形ABCD的面積;
正方形ABCD的面積;
⑶正確.BE+BF=AB= ![]() OA;
OA;
⑷正確.
AE2+CF2=BE2+BF2=EF2=( ![]() OF)2=2OF2,
OF)2=2OF2,
在△OPF與△OFB中,
∠OBF=∠OFP=45°,
∠POF=∠FOB,
∴△OPF∽△OFB,
OP:OF=OF:OB,
OF2=OPOB,
AE2+CF2=20POB.
另法:AE2+CF2=BF2+BE2=EF2=(PF+PE)2=PE2+PF2+2PEPF.
作OM⊥EF,M為垂足.
∵OE=OF,
∴OM=ME=MF.
PE2+PF2=(ME﹣MP)2+(MF+MP)2=2(MO2+MP2)=2OP2.
∵O、E、B、F四點共圓,
∴PEPF=OPPB,
∴AE2+CF2=2OP2+2OPPB=2OP(OP+PB)=2OPOB.
所以答案是:C.
【考點精析】解答此題的關鍵在于理解勾股定理的概念的相關知識,掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2,以及對正方形的性質的理解,了解正方形四個角都是直角,四條邊都相等;正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角;正方形的一條對角線把正方形分成兩個全等的等腰直角三角形;正方形的對角線與邊的夾角是45o;正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,![]() 的位置如圖所示.
的位置如圖所示.
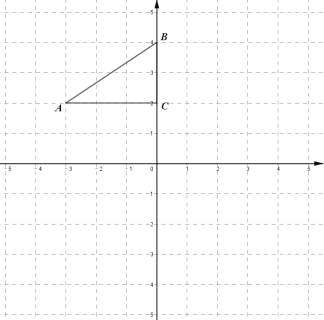
(1)畫出![]() 先向右平移3個單位,再向下平移6個單位后得到的
先向右平移3個單位,再向下平移6個單位后得到的![]() ,并寫出
,并寫出![]() ,各頂點的坐標;
,各頂點的坐標;
(2)畫出![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 后得到的
后得到的![]() ,并寫出
,并寫出![]() ,各頂點的坐標.
,各頂點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商貿公司有![]() 、
、![]() 兩種型號的商品需運出,這兩種商品的體積和質量分別如下表所示:
兩種型號的商品需運出,這兩種商品的體積和質量分別如下表所示:
體積(立方米/件) | 質量(噸/件) | |
| 0.8 | 0.5 |
| 2 | 1 |
(1)已知一批商品有![]() 、
、![]() 兩種型號,體積一共是20立方米,質量一共是10.5噸,求
兩種型號,體積一共是20立方米,質量一共是10.5噸,求![]() 、
、![]() 兩種型號商品各有幾件?
兩種型號商品各有幾件?
(2)物資公司現有可供使用的貨車每輛額定載重3.5噸,容積為6立方米,其收費方式有以下兩種:
①按車收費:每輛車運輸貨物到目的地收費600元;
②按噸收費:每噸貨物運輸到目的地收費200元.
現要將(1)中商品一次或分批運輸到目的地,如果兩種收費方式可混合使用,商貿公司應如何選擇運送、付費方式,使其所花運費最少,最少運費是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果一個多位自然數的任意兩個相鄰數位上,右邊數位上的數總比左邊數位上的數大1,則我們稱這樣的自然數叫“美數”,例如:123,3456,67,…都是“美數”.
(1)若某個三位“美數”恰好等于其個位的76倍,這個“美數”為 .
(2)證明:任意一個四位“美數”減去任意一個兩位“美數”之差再減去1得到的結果定能被11整除;
(3)如果一個多位自然數的任意兩個相鄰數位上,左邊數位上的數總比右邊數位上的數大1,則我們稱這樣的自然數叫“妙數”,若任意一個十位為![]()
![]() 為整數)的兩位“妙數”和任意一個個位為
為整數)的兩位“妙數”和任意一個個位為![]() 為整數)的兩位“美數”之和為55,則稱兩位數
為整數)的兩位“美數”之和為55,則稱兩位數![]() 為“美妙數”,并把這個“美妙數”記為
為“美妙數”,并把這個“美妙數”記為![]() ,則求
,則求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一矩形紙片OABC放在直角坐標系中,O為原點,C在x軸上,OA=6,OC=10.
(Ⅰ)如圖①,在OA上取一點E,將△EOC沿EC折疊,使點O落在AB邊上的D點,求E點的坐標;
(Ⅱ)如圖②,在OA、OC邊上選取適當的點E′、F,將△E′OF沿E′F折疊,使O點落在AB邊上D′點,過D′作D′G∥OA交E′F于T點,交OC于G點,設T的坐標為(x,y),求y與x之間的函數關系式,并直接寫出自變量x的取值范圍;
(Ⅲ)在(Ⅱ)的條件下,若OG=2 ![]() ,求△D′TF的面積.(直接寫出結果即可)
,求△D′TF的面積.(直接寫出結果即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙兩地相距50千米.星期天上午8:00小聰同學在父親陪同下騎山地車從甲地前往乙地.2小時后,小明的父親騎摩托車沿同一路線也從甲地前往乙地,他們行駛的路程y(千米)與小聰行駛的時間x(小時)之間的函數關系如圖所示,小明父親出發小時時,行進中的兩車相距8千米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形 ACDE 是證明勾股定理時用到的一個圖形,a 、b 、c 是 RtABC和 RtBED 的邊長,已知![]() ,這時我們把關于 x 的形如
,這時我們把關于 x 的形如![]() 二次方程稱為“勾系一元二次方程”.
二次方程稱為“勾系一元二次方程”.

請解決下列問題:
(1)寫出一個“勾系一元二次方程”;
(2)求證:關于 x 的“勾系一元二次方程”![]() ,必有實數根;
,必有實數根;
(3)若 x 1是“勾系一元二次方程” ![]() 的一個根,且四邊形 ACDE 的周長是6
的一個根,且四邊形 ACDE 的周長是6![]() ,求ABC 的面積.
,求ABC 的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,邊長為4的等邊三角形AOB的頂點O在坐標原點,點A在x軸的正半軸上,點B在第一象限.點P從點O出發,沿x軸以每秒1個單位長的速度向點A勻速運動,當點P到達點A時停止運動,設點P運動的時間是t秒.將線段BP的中點繞點P按順時針方向旋轉60°得點C,點C隨點P的運動而運動,連接CP、CA.過點P作PD⊥OB于D點
(1)直接寫出BD的長并求出點C的坐標(用含t的代數式表示)
(2)在點P從O向A運動的過程中,△PCA能否成為直角三角形?若能,求t的值.若不能,請說明理由;
(3)點P從點O運動到點A時,點C運動路線的長是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=﹣x2+2x+3與x軸交于A、B兩點(點A在點B的左邊),與y軸交于點C,連接BC.
(1)求A、B、C三點的坐標及拋物線的對稱軸;
(2)若已知x軸上一點N( ![]() ,0),則在拋物線的對稱軸上是否存在一點Q,使得△CNQ是直角三角形?若存在,求出點Q的坐標;若不存在,請說明理由.
,0),則在拋物線的對稱軸上是否存在一點Q,使得△CNQ是直角三角形?若存在,求出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com