【題目】下列計算正確的是( )
A. a3a2=a6 B. (﹣a2)3=a6 C. a3+a4=a7 D. a2(a3)4=a14
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】某籃球隊在一次聯賽中共進行了10場比賽，已知10場比賽的平均得分為88分，且前9場比賽的得分依次為：97、91、85、91、84、86、85、82、88．
（1）求第10場比賽的得分；
（2）求這10場比賽得分的中位數，眾數和方差．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知AB∥CD，分別探討下面四個圖形中∠APC與∠PAB，∠PCD之間的關系，請你從所得到的關系中任選一個加以證明。
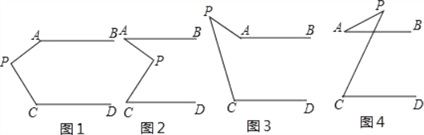
（1）在圖1中，∠APC與∠PAB，∠PCD之間的關系是： ．
（2）在圖2中，∠APC與∠PAB，∠PCD之間的關系是： ．
（3）在圖3中，∠APC與∠PAB，∠PCD之間的關系是： ．
（4）在圖4中，∠APC與∠PAB，∠PCD之間的關系是： ．
（5）在圖 中，求證： ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校九年級學生參加體育測試，其中10人的引體向上成績如下表：
完成引體向上的個數 | 7 | 8 | 9 | 10 |
人數 | 1 | 2 | 3 | 4 |
這10人完成引體向上個數的中位數是___________
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知關于x的一元二次方程x2﹣2x+m+2=0有兩個不等的實數根x1和x2
（1）求m的取值范圍并證明x1x2=m+2；
（2）若|x1﹣x2|=2，求m的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
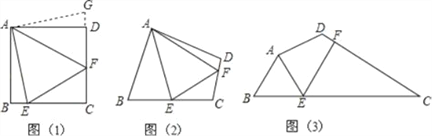
【題目】問題：如圖(1)，點E、F分別在正方形ABCD的邊BC、CD上，∠EAF=45°，試判斷BE、EF、FD之間的數量關系．
【發現證明】小聰把△ABE繞點A逆時針旋轉90°至△ADG,從而發現EF=BE+FD,請你利用圖（1）證明上述結論．
【類比引申】如圖(2)，四邊形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,點E、F分別在邊BC、CD上,則當∠EAF與∠BAD滿足 關系時，仍有EF=BE+FD．
【探究應用】如圖(3)，在某公園的同一水平面上，四條通道圍成四邊形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分別有景點E、F，且AE⊥AD，DF=40（
﹣1）米，現要在E、F之間修一條筆直道路，求這條道路EF的長（結果取整數，參考數據： 
=1.41， 
=1.73）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
