
【題目】已知,在![]() 中,
中,![]() ,
,![]() 于點
于點![]() ,
,![]() 分別交
分別交![]() 、
、![]() 于點
于點![]() 、點
、點![]() ,連接
,連接![]() ,若
,若![]() .
.
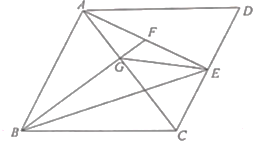
(1)若![]() ,求
,求![]() 的面積.
的面積.
(2)求證:![]() .
.
【答案】(1)72;(2)見解析.
【解析】
(1)由![]() 得AB=CD,AD=BC,AB∥CD,則∠BAG=∠ACE,由
得AB=CD,AD=BC,AB∥CD,則∠BAG=∠ACE,由![]() 得∠ACE+∠EAC=90°,則∠BAG+∠EAC=∠BAE =90°,由
得∠ACE+∠EAC=90°,則∠BAG+∠EAC=∠BAE =90°,由![]() ,
,![]() 可證得∠AFB=∠ACE,又因為BF=BC,
可證得∠AFB=∠ACE,又因為BF=BC,![]() 可得BF=AC,可證△ABF≌△EAC,則AB=AE,
可得BF=AC,可證△ABF≌△EAC,則AB=AE,![]() 的面積=AECD=
的面積=AECD=![]() ,在Rt△ABE中,由BE=12即可求得
,在Rt△ABE中,由BE=12即可求得![]() ;
;
(2)由(1)知:△ABF≌△EAC,得△EAD≌△EAC,設CE=x,則AB=CD=2x,BF=AD=![]() x,根據面積法計算AG的長,作高線GH,利用三角函數分別得EH和GH的長,利用勾股定理計算EG的長,代入結論化簡可得結論.
x,根據面積法計算AG的長,作高線GH,利用三角函數分別得EH和GH的長,利用勾股定理計算EG的長,代入結論化簡可得結論.
(1)解:∵![]() ,
,
∴AB=CD,AD=BC,AB∥CD,
∴∠BAG=∠ACE,
∵![]() ,
,
∴∠ACE+∠EAC=90°,
∴∠BAG+∠EAC=∠BAE =90°,
∵![]() ,
,![]() ,
,
∴∠AFB=∠ACE,∠AEC =∠BAE =90°,
∵BF=BC,![]() ,
,
∴BF=AC,
∴△ABF≌△EAC,
∴AB=AE,
∴![]() 的面積=AECD=
的面積=AECD=![]() ,
,
在Rt△ABE中, BE=12
∴2![]() =
=![]()
![]() =72,
=72,
∴![]() 的面積=72;
的面積=72;
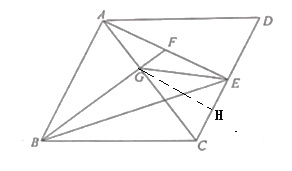
(2)證明:由(1)知:△ABF≌△EAC,
∵BF=BC=AD,
∴△EAD≌△EAC,
∴AF=DE=CE,AE=AB=2CE,
設CE=x,則AB=CD=2x,BF=AD=![]() x,,
x,,
S△ABF=![]() BFAG=
BFAG=![]() AFAB,
AFAB,![]() xAG=x2x,
xAG=x2x,
∴AG=![]() x,
x,
∴CG=![]() x-
x-![]() x=
x=![]() x,
x,
過G作GH⊥CD于H,
sin∠ECG=![]() =
=![]() ,
,
∴GH=![]() x,
x,
cos∠ECG=![]() =
=![]() ,
,
CH=![]() x,
x,
∴EH=x-![]() x=
x=![]() ,
,
∴EG=![]() =
=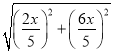 =
=![]() ,
,
∴![]() =
=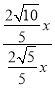 =
=![]() ,
,
∴GE=![]() AG.
AG.
故答案為:(1)72;(2)見解析.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:初中數學 來源: 題型:
【題目】我市晶泰星公司安排![]() 名工人生產甲、乙兩種產品,每人每天生產
名工人生產甲、乙兩種產品,每人每天生產![]() 件甲產品或
件甲產品或![]() 件乙產品.根據市場行情測得,甲產品每件可獲利
件乙產品.根據市場行情測得,甲產品每件可獲利![]() 元,乙產品每件可獲利
元,乙產品每件可獲利![]() 元.而實際生產中,生產乙產品需要數外支出一定的費用,經過核算,每生產
元.而實際生產中,生產乙產品需要數外支出一定的費用,經過核算,每生產![]() 件乙產品,當天每件乙產品平均荻利減少
件乙產品,當天每件乙產品平均荻利減少![]() 元,設每天安排
元,設每天安排![]() 人生產乙產品.
人生產乙產品.
(1)根據信息填表:
產品種類 | 每天工人數(人) | 每天產量(件) | 每件產品可獲利潤(元) |
甲 |
| ||
乙 |
|
|
(2)若每天生產甲產品可獲得的利潤比生產乙產品可獲得的利潤多![]() 元,試問:該企業(yè)每天生產甲、乙產品可獲得總利潤是多少元?
元,試問:該企業(yè)每天生產甲、乙產品可獲得總利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】七年級一班和二班各推選![]() 名同學進行投籃比賽,按照比賽規(guī)則,每人各投了
名同學進行投籃比賽,按照比賽規(guī)則,每人各投了![]() 個球,兩個班選手的進球數統(tǒng)計如下表,請根據表中數據回答問題.
個球,兩個班選手的進球數統(tǒng)計如下表,請根據表中數據回答問題.
進球數(個) |
|
|
|
|
|
|
一班人數(人) |
|
|
|
|
|
|
二班人數(人) |
|
|
|
|
|
|
![]() 填表;
填表;
平均數 | 中位數 | 眾數 | 方差 | |
一班 | 2.6 | |||
二班 | 7 | 7 | 7 |
![]() 如果要從這兩個班中選出一個班代表級部參加學校的投籃比賽,爭取奪得總進球數團體第一名,你認為應該選擇哪個班?如果要爭取個人進球數進入學校前三名,你認為應該選擇哪個班?
如果要從這兩個班中選出一個班代表級部參加學校的投籃比賽,爭取奪得總進球數團體第一名,你認為應該選擇哪個班?如果要爭取個人進球數進入學校前三名,你認為應該選擇哪個班?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,已知AB=AC=10cm,BC=16cm,AD⊥BC于D,點E、F分別從B、C兩點同時出發(fā),其中點E沿BC向終點C運動,速度為4cm/s;點F沿CA、AB向終點B運動,速度為5cm/s,設它們運動的時間為x(s).
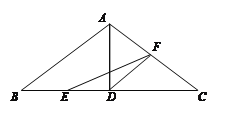
(1)求x為何值時,△EFC和△ACD相似;
(2)是否存在某一時刻,使得△EFD被 AD分得的兩部分面積之比為3:5,若存在,求出x的值,若不存在,請說明理由;
(3)若以EF為直徑的圓與線段AC只有一個公共點,求出相應x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
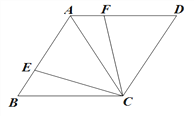
【題目】如圖,四邊形ABCD中,∠B=60°,對角線AC=BC,點E在AB上,將CE繞點C順時針旋轉60得CF,且點F在AD上.
(1)求證:AF=BE;
(2)若AE=DF,求證:四邊形ABCD是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知過點B(1,0)的直線![]() 與直線
與直線![]() :
:![]() 相交于點P(-1,a).且l1與y軸相交于C點,l2與x軸相交于A點.
相交于點P(-1,a).且l1與y軸相交于C點,l2與x軸相交于A點.
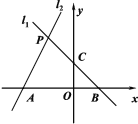
(1)求直線![]() 的解析式;
的解析式;
(2)求四邊形![]() 的面積;
的面積;
(3)若點Q是x軸上一動點,連接PQ、CQ,當△QPC周長最小時,求點Q坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB∥CD,EF與AB,CD分別交于點G,H,∠CHG的平分線HM交AB于點M,若∠EGB=50°,則∠GMH的度數為( )
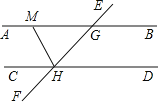
A. 50°B. 55°C. 60°D. 65°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,直線y=﹣![]() x+b與x軸、y軸相交于A、B兩點,動點C(m,0)在線段OA上,將線段CB繞著點C順時針旋轉90°得到CD,此時點D恰好落在直線AB上,過點D作DE⊥x軸于點E.
x+b與x軸、y軸相交于A、B兩點,動點C(m,0)在線段OA上,將線段CB繞著點C順時針旋轉90°得到CD,此時點D恰好落在直線AB上,過點D作DE⊥x軸于點E.
(1)求m和b的數量關系;
(2)當m=1時,如圖2,將△BCD沿x軸正方向平移得△B′C′D′,當直線B′C′經過點D時,求點B′的坐標及△BCD平移的距離;
(3)在(2)的條件下,直線AB上是否存在一點P,以P、C、D為頂點的三角形是等腰直角三角形?若存在,寫出滿足條件的P點坐標;若不存在,請說明理由.

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com