
【題目】如圖,菱形![]() 的邊長為1,
的邊長為1,![]() ,點E是邊
,點E是邊![]() 上任意一點(端點除外),線段
上任意一點(端點除外),線段![]() 的垂直平分線交
的垂直平分線交![]() ,
,![]() 分別于點F,G,
分別于點F,G,![]() ,
,![]() 的中點分別為M,N.
的中點分別為M,N.
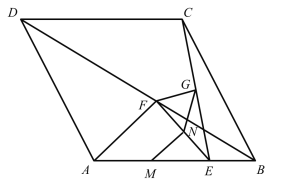
(1)求證:![]() ;
;
(2)求![]() 的最小值;
的最小值;
(3)當點E在![]() 上運動時,
上運動時,![]() 的大小是否變化?為什么?
的大小是否變化?為什么?
【答案】(1)見解析;(2)![]() ;(3)不變,理由見解析.
;(3)不變,理由見解析.
【解析】
(1)連接CF,根據垂直平分線的性質和菱形的對稱性得到CF=EF和CF=AF即可得證;
(2)連接AC,根據菱形對稱性得到AF+CF最小值為AC,再根據中位線的性質得到MN+NG的最小值為AC的一半,即可求解;
(3)延長EF,交DC于H,利用外角的性質證明∠AFC=∠FCE+∠FEC+∠FAE+∠FEA,再由AF=CF=EF,得到∠AEF=∠EAF,∠FEC=∠FCE,從而推斷出∠AFD=∠FAE+∠ABF=∠FAE+∠CEF,從而可求出∠ABF=∠CEF=30°,即可證明.
解:(1)連接CF,
∵FG垂直平分CE,
∴CF=EF,
∵四邊形ABCD為菱形,
∴A和C關于對角線BD對稱,
∴CF=AF,
∴AF=EF;
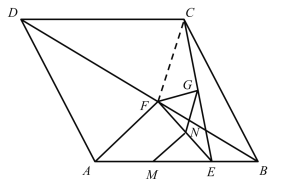
(2)連接AC,
∵M和N分別是AE和EF的中點,點G為CE中點,
∴MN=![]() AF,NG=
AF,NG=![]() CF,即MN+NG=
CF,即MN+NG=![]() (AF+CF),
(AF+CF),
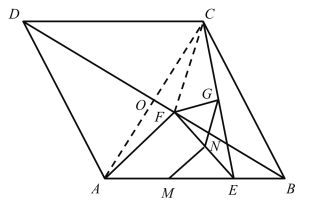
當點F與菱形ABCD對角線交點O重合時,
AF+CF最小,即此時MN+NG最小,
∵菱形ABCD邊長為1,∠ABC=60°,
∴△ABC為等邊三角形,AC=AB=1,
即MN+NG的最小值為![]() ;
;
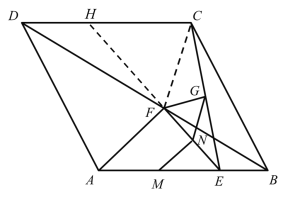
(3)不變,理由是:
延長EF,交DC于H,
∵∠CFH=∠FCE+∠FEC,∠AFH=∠FAE+∠FEA,
∴∠AFC=∠FCE+∠FEC+∠FAE+∠FEA,
∵點F在菱形ABCD對角線BD上,根據菱形的對稱性可得:
∠AFD=∠CFD=![]() ∠AFC,
∠AFC,
∵AF=CF=EF,
∴∠AEF=∠EAF,∠FEC=∠FCE,
∴∠AFD=∠FAE+∠ABF=∠FAE+∠CEF,
∴∠ABF=∠CEF,
∵∠ABC=60°,
∴∠ABF=∠CEF=30°,為定值.


科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點![]() 、
、![]() 的坐標分別為
的坐標分別為![]() 、
、![]() ,點
,點![]() 在第一象限內,
在第一象限內,![]() ,
,![]() ,函數
,函數![]() 的圖像經過點
的圖像經過點![]() ,將
,將![]() 沿
沿![]() 軸的正方向向右平移
軸的正方向向右平移![]() 個單位長度,使點
個單位長度,使點![]() 恰好落在函數
恰好落在函數![]() 的圖像上,則
的圖像上,則![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.3D.
C.3D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公園的門票價格如表:
購票人數 | 1~50 | 51~100 | 100以上 |
門票價格 | 13元/人 | 11元/人 | 9元/人 |
現某單位要組織其市場部和生產部的員工游覽該公園,這兩個部門人數分別為a和b(a≥b).若按部門作為團體,選擇兩個不同的時間分別購票游覽公園,則共需支付門票費為1290元;若兩個部門合在一起作為一個團體,同一時間購票游覽公園,則共需支付門票費為990元,那么這兩個部門的人數a=_____;b=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
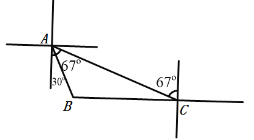
【題目】如圖,觀測站C發現在它的正西方向,有一艘漁船B出現險情,需救援,當即上報救援中心A,測得C在A的南偏東67方向,距A處50海里,而B在A的南偏東30方向,求漁船B與救援中心A的距離AB,漁船B與觀測站C的距離BC.(結果精確到0.1海里)(參考數據:sin37=0.6,cos37=0.8,tan37=![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2020年是脫貧攻堅年,為實現全員脫貧目標,某村貧困戶在當地政府支持幫助下,辦起了養雞場,經過一段時間精心飼養,總量為3000只的一批雞可以出售.現從中隨機抽取50只,得到它們質量的統計數據如下:
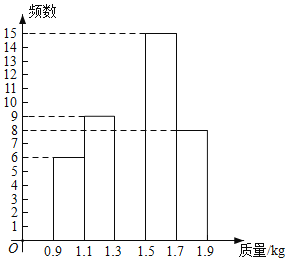
質量 | 組中值 | 數量(只) |
| 1.0 | 6 |
| 1.2 | 9 |
| 1.4 | a |
| 1.6 | 15 |
| 1.8 | 8 |
根據以上信息,解答下列問題:
(1)表中![]() ______,補全頻數分布直方圖;
______,補全頻數分布直方圖;
(2)這批雞中質量不小于![]() 的大約有多少只?
的大約有多少只?
(3)這些貧因戶的總收入達到54000元,就能實現全員脫貧目標.按15元![]() 的價格售出這批雞后,該村貧困戶能否脫貧?
的價格售出這批雞后,該村貧困戶能否脫貧?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】AB是![]() 的直徑,點C是
的直徑,點C是![]() 上一點,連接AC、BC,直線MN過點C,滿足
上一點,連接AC、BC,直線MN過點C,滿足![]() .
.
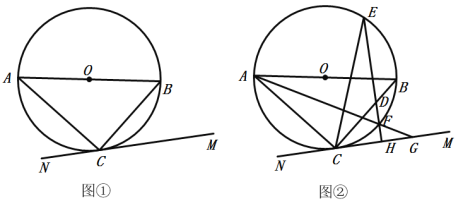
(1)如圖①,求證:直線MN是![]() 的切線;
的切線;
(2)如圖②,點D在線段BC上,過點D作![]() 于點H,直線DH交
于點H,直線DH交![]() 于點E、F,連接AF并延長交直線MN于點G,連接CE,且
于點E、F,連接AF并延長交直線MN于點G,連接CE,且![]() ,若
,若![]() 的半徑為1,
的半徑為1,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
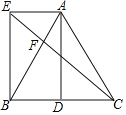
【題目】如圖,在△ABC中,AB=AC,D為BC中點,AE∥BD,且AE=BD.
(1)求證:四邊形AEBD是矩形;
(2)連接CE交AB于點F,若∠ABE=30°,AE=2,求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為迎接:“國家衛生城市”復檢,某市壞衛局準備購買A、B兩種型號的垃圾箱,通過市場調研得知:購買3個A型垃圾箱和2個B型垃圾箱共需540元,購買2個A型垃圾箱比購買3個B型垃圾箱少用160元.
(1)求每個A型垃圾箱和B型垃圾箱各多少元?
(2)該市現需要購A、B買兩種型號的垃圾箱共30個,其中買A型垃圾箱不超過16個.求出購買費用最少時的購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
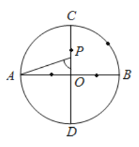
【題目】如圖,![]() 是
是![]() 的兩條互相垂直的直徑,點P從點O出發,沿
的兩條互相垂直的直徑,點P從點O出發,沿![]() 的路線勻速運動,設
的路線勻速運動,設![]() (單位:度),那么y與點P運動的時間(單位:秒)的關系圖是( )
(單位:度),那么y與點P運動的時間(單位:秒)的關系圖是( )
A.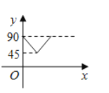 B.
B.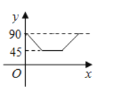 C.
C.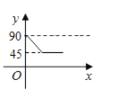 D.
D.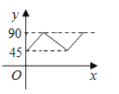
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com