
【題目】小明在復習數學知識時,針對“求一元二次方程的解”,整理了以下的幾種方法,請你將有關內容補充完整.例題:求一元二次方程![]() 的兩個解.
的兩個解.
(1)解法一:選擇合適的一種方法(公式法、配方法、分解因式法)求解.解方程:![]() ;
;
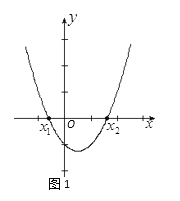
(2)解法二:利用二次函數圖象與坐標軸的交點求解,如圖1所示,把方程![]() 的解看成是二次函數y= 的圖象與x軸交點的橫坐標,即x1,x2就是方程的解.
的解看成是二次函數y= 的圖象與x軸交點的橫坐標,即x1,x2就是方程的解.
(3)解法三:利用兩個函數圖象的交點求解.
①把方程![]() 的解看成是一個二次函數y= 的圖象與一個一次函數y= 的圖象交點的橫坐標;
的解看成是一個二次函數y= 的圖象與一個一次函數y= 的圖象交點的橫坐標;
②畫出這兩個函數的圖象,用x1,x2在x軸上標出方程的解.
【答案】(1)過程見解析,![]() =
=![]() ,
,![]() =
=![]() ;(2)
;(2)![]() ;(3)①
;(3)①![]() ,
,![]() ;②見解析
;②見解析
【解析】
(1)利用公式法求解即可.
(2)因為![]() 表示的是函數
表示的是函數![]() 與
與![]() 軸交點時的情境,即函數
軸交點時的情境,即函數![]() 的值為0時,所以把方程
的值為0時,所以把方程![]() 的解看成是二次函數
的解看成是二次函數![]() 的圖象與軸
的圖象與軸![]() 交點的橫坐標,可以得到答案.
交點的橫坐標,可以得到答案.
(3)①由![]() 變形為
變形為![]() ,因為
,因為![]() 都是變量
都是變量![]() 的函數,所以
的函數,所以![]() ,當兩個函數的函數值相等,即此時的函數值為兩個函數的交點的縱坐標,從而觀察圖像可以得到交點的橫坐標得到答案.
,當兩個函數的函數值相等,即此時的函數值為兩個函數的交點的縱坐標,從而觀察圖像可以得到交點的橫坐標得到答案.
②利用一次函數與二次函數的作圖方法在同一直角坐標系中作出圖像即可.
解:(1)解:∵![]() ,
,
∴![]() .∴
.∴![]() .
.
∴原方程的解是![]() =
=![]() ,
,![]() =
=![]() .
.
(2)因為求二次函數.![]() 與
與![]() 軸交點時,把交點的縱坐標
軸交點時,把交點的縱坐標![]() 代入函數解析式得到
代入函數解析式得到![]() 的解是交點的橫坐標,所以求方程
的解是交點的橫坐標,所以求方程![]() 的解時就可以畫出
的解時就可以畫出![]() 的圖像,觀察交點的橫坐標就是方程
的圖像,觀察交點的橫坐標就是方程![]() 的解.
的解.
故答案為![]() .
.
(3)因為![]() ,
,
所以![]() ,因為
,因為![]() 都是變量
都是變量![]() 的函數,
的函數,
建立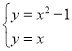
考查的兩個函數分別是![]() ,兩個函數的交點的橫坐標就是方程
,兩個函數的交點的橫坐標就是方程![]() 的解.
的解.
故答案為:![]() 與
與![]() ..
..
每畫出正確函數圖象如下:


 經典密卷系列答案
經典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案科目:初中數學 來源: 題型:
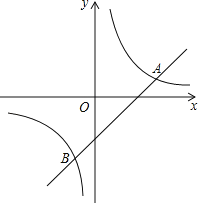
【題目】如圖,在平面直角坐標系xOy中,直線y=x﹣2與雙曲線y=![]() (k≠0)相交于A,B兩點,且點A的橫坐標是3.
(k≠0)相交于A,B兩點,且點A的橫坐標是3.
(1)求k的值;
(2)過點P(0,n)作直線,使直線與x軸平行,直線與直線y=x﹣2交于點M,與雙曲線y=![]() (k≠0)交于點N,若點M在N右邊,求n的取值范圍.
(k≠0)交于點N,若點M在N右邊,求n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將拋物線y=﹣x2向左平移3個單位,再向上平移4個單位.
(1)寫出平移后的拋物線的函數關系式.
(2)若平移后的拋物線的頂點為A,與x軸的兩個交點分別是B、C,求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2016廣西賀州市)如圖,將線段AB繞點O順時針旋轉90°得到線段A′B′,那么A(﹣2,5)的對應點A′的坐標是( )

A. (2,5) B. (5,2) C. (2,﹣5) D. (5,﹣2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在Rt△OAC中,∠OCA=90°,O為坐標原點,直角頂點C在x軸的正半軸上,反比例函數y=![]() (k>0)在第一象限的圖象經過OA的中點B,交AC于點D,連接OD.若∠A=∠COD,則直線OA的解析式為______.
(k>0)在第一象限的圖象經過OA的中點B,交AC于點D,連接OD.若∠A=∠COD,則直線OA的解析式為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,∠BAC=α,點D在邊AC上(不與點A,C重合)連接BD,點K為線段BD的中點,過點D作DE⊥AB于點E,連結CK,EK,CE,將△ADE繞點A順時針旋轉一定的角度(旋轉角小于90°)

(1)如圖1,若α=45°,則△ECK的形狀為______;
(2)在(1)的條件下,若將圖1中的△ADE繞點A旋轉,使得D,E,B三點共線,點K為線段BD的中點,如圖2所示,求證:BE-AE=2CK;
(3)若△ADE繞點A旋轉至圖3位置時,使得D,E,B三點共線,點K仍為線段BD的中點,請你直接寫出BE,AE,CK三者之間的數量關系(用含α的三角函數表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近幾年購物的支付方式日益增多,某數學興趣小組就此進行了抽樣調查.調查結果顯示,支付方式有:A微信、B支付寶、C現金、D其他,該小組對某超市一天內購買者的支付方式進行調查統計,得到如下兩幅不完整的統計圖.

請你根據統計圖提供的信息,解答下列問題:
(1)本次一共調查了多少名購買者?
(2)請補全條形統計圖;在扇形統計圖中A種支付方式所對應的圓心角為 度.
(3)若該超市這一周內有1600名購買者,請你估計使用A和B兩種支付方式的購買者共有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為支持國家南水北調工程建設,小王家由原來養殖戶變為種植戶,經市場調查得知,當種植櫻桃的面積x不超過15畝時,每畝可獲得利潤y=1900元;超過15畝時,每畝獲得利潤y(元)與種植面積x(畝)之間的函數關系如下表(為所學過的一次函數,反比例函數或二次函數中的一種)
x(畝) | 20 | 25 | 30 | 35 |
y(元) | 1800 | 1700 | 1600 | 1500 |
(1)請求出種植櫻桃的面積超過15畝時每畝獲得利潤y與x的函數關系式;
(2)如果小王家計劃承包荒山種植櫻桃,受條件限制種植櫻桃面積x不超過50畝,設小王家種植x畝櫻桃所獲得的總利潤為W元,求小王家承包多少畝荒山獲得的總利潤最大,并求總利潤W(元)的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com