
【題目】如圖1,已知二次函數y=mx2+3mx﹣![]() m的圖象與x軸交于A,B兩點(點A在點B的左側),頂點D和點B關于過點A的直線l:y=﹣
m的圖象與x軸交于A,B兩點(點A在點B的左側),頂點D和點B關于過點A的直線l:y=﹣![]() x﹣
x﹣![]() 對稱.
對稱.
(1)求A、B兩點的坐標及二次函數解析式;
(2)如圖2,作直線AD,過點B作AD的平行線交直線1于點E,若點P是直線AD上的一動點,點Q是直線AE上的一動點.連接DQ、QP、PE,試求DQ+QP+PE的最小值;若不存在,請說明理由:
(3)將二次函數圖象向右平移![]() 個單位,再向上平移3
個單位,再向上平移3![]() 個單位,平移后的二次函數圖象上存在一點M,其橫坐標為3,在y軸上是否存在點F,使得∠MAF=45°?若存在,請求出點F坐標;若不存在,請說明理由.
個單位,平移后的二次函數圖象上存在一點M,其橫坐標為3,在y軸上是否存在點F,使得∠MAF=45°?若存在,請求出點F坐標;若不存在,請說明理由.

【答案】(1)A(﹣![]() ,0),B(
,0),B(![]() ,0);拋物線解析式y=
,0);拋物線解析式y=![]() x2+
x2+![]() x﹣
x﹣![]() ;(2)12;(3)(0,
;(2)12;(3)(0,![]() ),(0,﹣
),(0,﹣![]() )
)
【解析】
(1)在y=mx2+3mx﹣![]() m中令y=0,解方程求得x的值即可求得A、B的坐標,繼而根據已知求出點D的坐標,把點D坐標代入函數解析式y=mx2+3mx﹣
m中令y=0,解方程求得x的值即可求得A、B的坐標,繼而根據已知求出點D的坐標,把點D坐標代入函數解析式y=mx2+3mx﹣![]() m利用待定系數法求得m即可得函數解析式;
m利用待定系數法求得m即可得函數解析式;
(2)先求出直線AD解析式,再根據直線BE∥AD,求得直線BE解析式,繼而可得點E坐標,如圖2,作點P關于AE 的對稱點P',作點E關于x軸的對稱點E',根據對稱性可得PQ=P'Q,PE=EP'=P'E',從而有DQ+PQ+PE=DQ+P'Q+P'E',可知當D,Q,E'三點共線時,DQ+PQ+PE值最小,即DQ+PQ+PE最小值為DE',根據D、E'坐標即可求得答案;
(3)分情況進行討論即可得答案.
(1)∵令y=0,
∴0=m x2+3mx﹣![]() m,
m,
∴x1=![]() ,x2=﹣
,x2=﹣![]() ,
,
∴A(﹣![]() ,0),B(
,0),B(![]() ,0),
,0),
∴頂點D的橫坐標為﹣![]() ,
,
∵直線y=﹣![]() x﹣
x﹣![]() 與x軸所成銳角為30°,且D,B關于y=﹣
與x軸所成銳角為30°,且D,B關于y=﹣![]() x﹣
x﹣![]() 對稱,
對稱,
∴∠DAB=60°,且D點橫坐標為﹣![]() ,
,
∴D(﹣![]() ,﹣3
,﹣3![]() ),
),
∴﹣3![]() =
=![]() m﹣
m﹣![]() m﹣
m﹣![]() m,
m,
∴m=![]() ,
,
∴拋物線解析式y=![]() x2+
x2+![]() x﹣
x﹣![]() ;
;
(2)∵A(﹣![]() ,0),D(﹣
,0),D(﹣![]() ,﹣3
,﹣3![]() ),
),
∴直線AD解析式y=﹣![]() x﹣
x﹣![]() ,
,
∵直線BE∥AD,
∴直線BE解析式y=﹣![]() x+
x+![]() ,
,
∴﹣![]() x﹣
x﹣![]() =﹣
=﹣![]() x+
x+![]() ,
,
∴x=![]() ,
,
∴E(![]() ,﹣3
,﹣3![]() ),
),
如圖2,作點P關于AE 的對稱點P',作點E關于x軸的對稱點E',
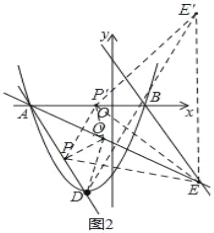
根據對稱性可得PQ=P'Q,PE=EP'=P'E',
∴DQ+PQ+PE=DQ+P'Q+P'E',
∴當D,Q,E'三點共線時,DQ+PQ+PE值最小,
即DQ+PQ+PE最小值為DE',
∵D(﹣![]() ,﹣3
,﹣3![]() ),E'(
),E'(![]() ,3
,3![]() ),
),
∴DE'=12,
∴DQ+PQ+PE最小值為12;
(3)∵拋物線y=![]() (x+
(x+![]() )2﹣3
)2﹣3![]() 圖象向右平移
圖象向右平移![]() 個單位,再向上平移3
個單位,再向上平移3![]() 個單位,
個單位,
∴平移后解析式y=![]() x2,
x2,
當x=3時,y=3![]() ,
,
∴M (3,3![]() ),
),
如圖3
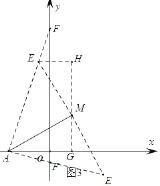
若以AM為直角邊,點M是直角頂點,在AM上方作等腰直角△AME,則∠EAM=45°,
直線AE交y軸于F點,作MG⊥x軸,EH⊥MG,則△EHM≌△AMG,
∵A(﹣![]() ,0),M(3,3
,0),M(3,3![]() ),
),
∴E(3﹣3![]() ,3
,3![]() +
+![]() ),
),
∴直線AE解析式:y=![]() x+
x+![]() ,
,
∴F(0,![]() ),
),
若以AM為直角邊,點M是直角頂點,在AM上方作等腰直角△AME,
同理可得:F(0,﹣![]() ).
).


科目:初中數學 來源: 題型:
【題目】如圖①,已知AB⊥BD,ED⊥BD,AB=CD,BC=DE
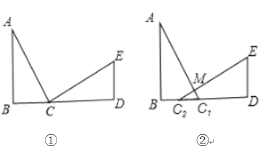
(1)求證:△ABC≌△CDE
(2)試判斷AC與CE的位置關系,并說明理由.
(3)若將CD沿CB方向平移得到圖②的情形,其余條件不變,此時第(2)問中AC與CE的位置關系還成立嗎?請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
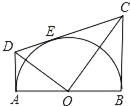
【題目】如圖,AB為半圓O的直徑,AD、BC分別切⊙O于A、B兩點,CD切⊙O于點E,AD與CD相交于D,BC與CD相交于C,連接OD、OC,對于下列結論:
①OD2=DECD;②AD+BC=CD;③OD=OC;④S梯形ABCD=![]() CDOA;⑤∠DOC=90°,
CDOA;⑤∠DOC=90°,
其中正確的是_____.(只需填上正確結論的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊△ABC的邊長為8,AD是BC邊上的中線,點E是AC邊上的一點,AE=2,若點M是線段AD上的一個動點,則ME+MC的最小值為____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,△ABC是邊長為3cm等邊三角形,動點P、Q分別同時從A、B兩點出發,分別沿AB、BC方向勻速移動,點P速度為1cm/s,點Q的速度為2cm/s,當點Q到達點C時,P、Q兩點停止運動,設點P的運動時間為t(s),
⑴當t為何值時,△PBQ是直角三角形?
⑵△PBQ能否成為等邊三角形?若能,請求出t值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,∠ABC=60°,AD、CE分別平分∠BAC、∠ACB,

(1)求∠AOC的度數
(2)連接BO,試說明BO平分∠ABC
(3)判斷AC、AE、CD的關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有A、B兩個港口,水由A流向B,水流的速度是4千米/小時,甲、乙兩船同時由A順流駛向B,各自不停地在A、B之間往返航行,甲在靜水中的速度是28千米/小時,乙在靜水中的速度是20千米/小時.

設甲行駛的時間為t小時,甲船距B港口的距離為S1千米,乙船距B港口的距離為S2千米,如圖為S1(千米)和t(小時)函數關系的部分圖象.
(1)A、B兩港口距離是_____千米.
(2)在圖中畫出乙船從出發到第一次返回A港口這段時間內,S2(千米)和t(小時)的函數關系的圖象.
(3)求甲、乙兩船第二次(不算開始時甲、乙在A處的那一次)相遇點M位于A、B港口的什么位置?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,輪船從B處以每小時60海里的速度沿南偏東20°方向勻速航行,在B處觀測燈塔A位于南偏東50°方向上,輪船航行20分鐘到達C處,在C處觀測燈塔A位于北偏東10°方向上,則C處與燈塔A的距離是___________海里.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在學校開展的數學活動課上,小明和小剛制作了一個正三樓錐(質量均勻,四個面完全相同),并在各個面上分別標記數字1,2,3,4,游戲規則如下每人投擲三棱錐兩次,并記錄底面的數字,如果兩次所擲數字的和為單數,那么算小明贏,如果兩歡所擲數字的和為偶數,那么算小明贏;
(1)請用列表或者面樹狀圍的方法表示上述游戲中的所有可能結果.
(2)請分別隸出小明和小剛能贏的概率,并判新游戲的公平性.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com