
已知一次函數(shù) 和反比例函數(shù)
和反比例函數(shù)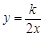 的圖象交于點(diǎn)A(1,1).
的圖象交于點(diǎn)A(1,1).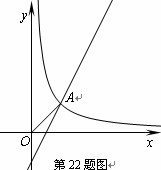
⑴求兩個(gè)函數(shù)的解析式;
⑵若點(diǎn)B是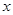 軸上一點(diǎn),且△AOB是直角三角形,求B點(diǎn)的坐標(biāo).
軸上一點(diǎn),且△AOB是直角三角形,求B點(diǎn)的坐標(biāo).
略
解析試題考查知識(shí)點(diǎn):求一次函數(shù)、反比例函數(shù)的解析式,直角三角形
思路分析:先求反比例函數(shù)的解析式,再求一次函數(shù)的解析式。根據(jù)要求構(gòu)建三角形,計(jì)算出OB的長(zhǎng)度
具體解答過(guò)程:
(1)、∵反比例函數(shù)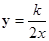 的圖象過(guò)點(diǎn)A(1,1)
的圖象過(guò)點(diǎn)A(1,1)
∴把x=1,y=1帶入到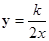 中求得k=2
中求得k=2
∴反比例函數(shù)的解析式為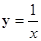
∵一次函數(shù)y=kx+b(k≠0)過(guò)點(diǎn)A(1,1)
∴把x=1,y=1帶入到y(tǒng)=kx+b(k≠0)中得:1=k+b
結(jié)合k=2,可求得b=-1
∴一次函數(shù)的解析式為y=2x-1
(2)、分兩種情況討論:
第一種情況:如下圖圖所示。過(guò)A點(diǎn)做BA⊥OA交x軸于B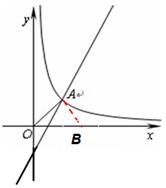
OA所在的直線過(guò)O(0,0)和A(1,1),不難看出直線OA的解析式為:y=x,且與x軸正半軸的夾角為45°,而OA的長(zhǎng)度為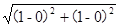 =
=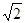
∴△OAB是以O(shè)A、AB為腰,OB為底的等腰直角三角形
∴OB=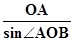 =
=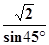 =2
=2
∴點(diǎn)B的坐標(biāo)為(0,2)
第二種情況:如下圖圖所示。過(guò)A點(diǎn)做AB⊥x軸,垂足為B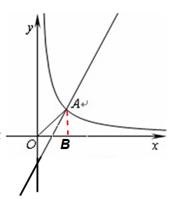
同樣的道理可以看出,△ABO為以O(shè)B、AB為腰,OA為底的等腰直角三角形,而
OB=OA·sin∠AOB=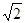 ×
×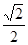 =1
=1
∴點(diǎn)B的坐標(biāo)為(0,1)
綜上所述,B點(diǎn)的坐標(biāo)為(0,2)或(0,1)
試題點(diǎn)評(píng):這是一道關(guān)于函數(shù)和三角形結(jié)合的綜合題目。


 通城學(xué)典默寫能手系列答案
通城學(xué)典默寫能手系列答案 金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案
金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
已知一次函數(shù)![]() 和反比例函數(shù)
和反比例函數(shù)![]() 的圖象交于點(diǎn)A(1,1)
的圖象交于點(diǎn)A(1,1)
(1) 求兩個(gè)函數(shù)的解析式;
(2) 若點(diǎn)B是![]() 軸上一點(diǎn),且△AOB是直角三角形,求B點(diǎn)的坐標(biāo)。
軸上一點(diǎn),且△AOB是直角三角形,求B點(diǎn)的坐標(biāo)。
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
已知一次函數(shù)![]() 和反比例函數(shù)
和反比例函數(shù)![]() 的圖象交于點(diǎn)A(1,1)
的圖象交于點(diǎn)A(1,1)
(1) 求兩個(gè)函數(shù)的解析式;
(2) 若點(diǎn)B是![]() 軸上一點(diǎn),且△AOB是直角三角形,求B點(diǎn)的坐標(biāo)。
軸上一點(diǎn),且△AOB是直角三角形,求B點(diǎn)的坐標(biāo)。
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2006-2007學(xué)年北京市師大附中九年級(jí)(上)期中數(shù)學(xué)試卷(解析版) 題型:解答題
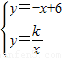 和反比例函數(shù)y=
和反比例函數(shù)y=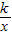 的圖象過(guò)點(diǎn)A,B,A點(diǎn)橫坐標(biāo)為x1,B點(diǎn)橫坐標(biāo)為x2,且2x2-x1=6,如圖所示.
的圖象過(guò)點(diǎn)A,B,A點(diǎn)橫坐標(biāo)為x1,B點(diǎn)橫坐標(biāo)為x2,且2x2-x1=6,如圖所示.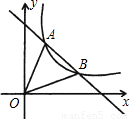
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2012年初中畢業(yè)升學(xué)考試(貴州黔西南卷)數(shù)學(xué)(解析版) 題型:選擇題
已知一次函數(shù) 和反比例函數(shù)
和反比例函數(shù) 的圖象在平面直角坐標(biāo)系中交于A、B兩點(diǎn),當(dāng)y1>y2時(shí),x的取值范圍是【 】
的圖象在平面直角坐標(biāo)系中交于A、B兩點(diǎn),當(dāng)y1>y2時(shí),x的取值范圍是【 】
(A)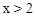 (B)
(B)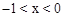 (C)
(C)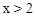 ,
,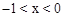 (D)
(D)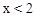 ,
,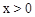

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2008年高級(jí)中等學(xué)校招生全國(guó)統(tǒng)一考試數(shù)學(xué)卷(廣東深圳) 題型:解答題
已知一次函數(shù)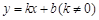 和反比例函數(shù)
和反比例函數(shù)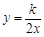 的圖象交于點(diǎn)A(1,1).
的圖象交于點(diǎn)A(1,1).

⑴求兩個(gè)函數(shù)的解析式;
⑵若點(diǎn)B是 軸上一點(diǎn),且△AOB是直角三角形,求B點(diǎn)的坐標(biāo).
軸上一點(diǎn),且△AOB是直角三角形,求B點(diǎn)的坐標(biāo).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com