
【題目】拋物線y=ax2+bx+c的對稱軸為直線x=﹣1,部分圖象如圖所示,下列判斷中:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若點(![]() ,y1),(﹣2,y2)均在拋物線上,則y1>y2;⑤5a﹣2b<0;其中正確的個數有( )
,y1),(﹣2,y2)均在拋物線上,則y1>y2;⑤5a﹣2b<0;其中正確的個數有( )
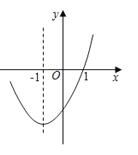
A.2B.3C.4D.5
【答案】A
【解析】
利用拋物線開口方向得到![]() ,利用拋物線的對稱軸方程得到
,利用拋物線的對稱軸方程得到![]() ,利用拋物線與
,利用拋物線與![]() 軸的交點位置得到
軸的交點位置得到![]() ,則可對①進行判斷;利用拋物線與
,則可對①進行判斷;利用拋物線與![]() 軸交點個數可對②進行判斷;利用拋物線的對稱性得到拋物線與
軸交點個數可對②進行判斷;利用拋物線的對稱性得到拋物線與![]() 軸的另一個交點坐標為
軸的另一個交點坐標為![]() ,則可對③進行判斷;根據二次函數的性質,通過比較兩點到對稱軸的距離可對④進行判斷;利用
,則可對③進行判斷;根據二次函數的性質,通過比較兩點到對稱軸的距離可對④進行判斷;利用![]() 得到
得到![]() ,則可對⑤進行判斷.
,則可對⑤進行判斷.
解:![]() 拋物線開口向上,
拋物線開口向上,
![]() ,
,
![]() 拋物線的對稱軸為直線
拋物線的對稱軸為直線![]() ,
,
![]() ,
,
![]() 拋物線與
拋物線與![]() 軸的交點在
軸的交點在![]() 軸下方,
軸下方,
![]() ,
,
![]() ,所以①錯誤;
,所以①錯誤;
![]() 拋物線與
拋物線與![]() 軸有2個交點,
軸有2個交點,
![]() △
△![]() ,所以②正確;
,所以②正確;
![]() 拋物線的對稱軸為直線
拋物線的對稱軸為直線![]() ,拋物線與
,拋物線與![]() 軸的一個交點坐標為
軸的一個交點坐標為![]() ,
,
![]() 拋物線與
拋物線與![]() 軸的另一個交點坐標為
軸的另一個交點坐標為![]() ,
,
![]() ,所以③正確;
,所以③正確;
![]() 點
點![]() 到直線
到直線![]() 的距離比點
的距離比點![]() 到直線
到直線![]() 的距離小,
的距離小,
而拋物線開口向上,
![]() ;所以④錯誤;
;所以④錯誤;
![]() ,
,
![]() ,所以⑤錯誤.
,所以⑤錯誤.
綜上所述:正確的有②③,共2個.
故選:![]() .
.


 導學教程高中新課標系列答案
導學教程高中新課標系列答案科目:初中數學 來源: 題型:
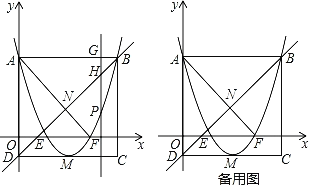
【題目】如圖,拋物線y=x2+bx+c經過A (0,3),B (4,3)兩點,與x軸交于點E,F,以AB為邊作矩形ABCD,其中CD邊經過拋物線的項點M,點P是拋物線上一動點(點P不與點A,B重合),過點P作y軸的平行線1與直線AB交于點G,與直線BD交于點H,連接AF交直線BD于點N.
(1)求該拋物線的解析式以及頂點M的坐標;
(2)當線段PH=2GH時,求點P的坐標;
(3)在拋物線上是否存在點P,使得以點P,E,N,F為頂點的四邊形是平行四邊形?若存在,請求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2022年北京冬奧會吉祥物“冰墩墩”以熊貓為原型進行設計創作,北京冬殘奧會吉祥物“雪容融”則以中國標志性符號的燈籠為創意進行設計創作“冰墩墩”和“雪容融”是一個非常完美的搭:配和組合,是中國文化和奧林匹克精神又一次完美的結合莉莉有“冰墩墩”和“雪容融”的紀念郵票各2張(如圖),這4張郵票背面完全相同,莉莉想給好友小婷和小華各送一張紀念郵票,她先讓小婷從這4張郵票中隨機抽取一張,然后,再讓小華從剩下的3張中隨機抽取一張.

(1)小婷抽到“冰墩墩”的紀念郵票的概率是__________.
(2)利用樹狀圖或列表法求小婷和小華均抽到“雪容融”的紀念郵票的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
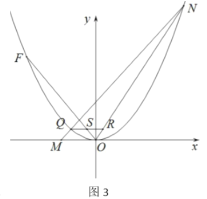
【題目】如圖 1,直線![]() 與
與![]() 軸,
軸,![]() 軸分別交于點
軸分別交于點![]() ,點
,點![]() ,拋物線
,拋物線![]() 經過點
經過點![]() ,點
,點![]() 和點
和點![]() ,并與直線
,并與直線![]() 交于另一點
交于另一點![]() .
.
(1)求拋物線![]() 的解析式;
的解析式;
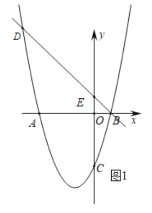
(2)如圖 2,點![]() 為
為![]() 軸上一動點,連接
軸上一動點,連接![]() ,當
,當![]() 時,求點
時,求點 ![]() 的坐標;
的坐標;
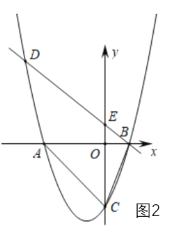
(3)如圖 3,將拋物線![]() 平移,使其頂點是坐標原點
平移,使其頂點是坐標原點![]() ,得到拋物線
,得到拋物線![]() ;將直線
;將直線![]() 向下平移經過坐標原點
向下平移經過坐標原點![]() ,交拋物線
,交拋物線![]() 于另一點
于另一點![]() .點
.點![]() ,點
,點![]() 是
是![]() 上且位于 第一象限內一動點,
上且位于 第一象限內一動點,![]() 交
交![]() 于
于![]() 點,
點,![]() 軸分別交
軸分別交![]() 于
于![]() ,試說明:
,試說明:![]() 與
與![]() 存在一個確定的數量關系.
存在一個確定的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
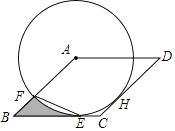
【題目】如圖,已知⊙A與菱形ABCD的邊BC相切于點E,與邊AB相交于點F,連接EF.
(1)求證:CD是⊙A的切線;
(2)若⊙A的半徑為2,tan∠BEF=![]() ,求圖中陰影部分的面積.
,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
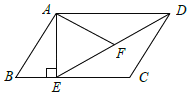
【題目】如圖,在平行四邊形ABCD中,過點A作AE⊥BC,垂足為E,連接DE,F為線段DE上一點,且∠AFE=∠B.
(1)求證:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的長.
,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
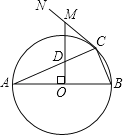
【題目】如圖,AB是⊙O的直徑,點C為⊙O上一點,CN為⊙O的切線,OM⊥AB于點O,分別交AC、CN于D、M兩點.
(1)求證:MD=MC;
(2)若⊙O的半徑為5,AC=4![]() ,求MC的長.
,求MC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
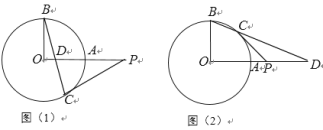
【題目】在⊙O中,半徑OA丄OB,點D在OA或OA的延長線上(不與點O,A重合),直線BD交⊙O于點C,過C作⊙O的切線交直線OA于點P.
(1)如圖(1),點D在線段OA上,若∠OBC=15°, 求∠OPC的大小;
(2)如圖(2),點D在OA的延長線上,若∠OBC=65°,求∠OPC的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com