
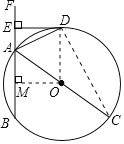
【題目】如圖所示,線段AC是⊙O的直徑,過A點作直線BF交⊙O于A、B兩點,過A點作∠FAC的角平分線交⊙O于D,過D作AF的垂線交AF于E.
(1)證明DE是⊙O的切線;
(2)證明AD2=2AEOA;
(3)若⊙O的直徑為10,DE+AE=4,求AB.

【答案】(1)證明見解析
(2)證明見解析
(3)8
【解析】
(1)連接OD,由![]() ,即可證明
,即可證明![]()
(2)連接CD,根據(jù)已知條件證明△ACD∽△ADE即可求解.
(3)過點O作OM⊥AB于點M,則四邊形ODEM為矩形,設(shè)DE=OM=x則AE=4﹣x,AM=5-(4﹣x)=1+x,在Rt△AMO中,OA2=AM2+OM2列出方程求解x再利用垂徑定理即可求解.
(1)證明:連接OD,
∵![]()
∴![]()
∵AD平分![]()
∴![]()
∴![]()
∴AF∥OD
又∵![]()
∴DE為⊙O切線;
(2)證明:連接CD.
∵AC為⊙O的直徑,DE⊥AF
∴∠ADC=90°,∠DEA=90°,
∴∠ADC=∠AED,
∴在△ACD和△ADE中,∠DAC=∠EAD,∠ADC=∠AED,
∴△ACD∽△ADE,
![]()
∴AD2=AEAC.
∵AC=2OA,
∴AD2=2AEOA;
(3)過點O作OM⊥AB于點M,則四邊形ODEM為矩形,設(shè)DE=OM=x,則AE=4﹣x,
∴AM=5﹣(4﹣x)=1+x,
在Rt△AMO中,OA2=AM2+OM2,即:(1+x)2+x2=52
解得:x1=3,x2=﹣4(舍去).
∴AM=4.
∵OM⊥AB,由垂徑定理得:AB=2AM=8.


科目:初中數(shù)學(xué) 來源: 題型:
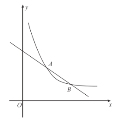
【題目】如圖,在平面直角坐標系![]() 中,一次函數(shù)
中,一次函數(shù)![]() 的圖象與反比例函數(shù)
的圖象與反比例函數(shù)![]() (
(![]() )的圖象交于
)的圖象交于![]() ,
,![]() 兩點.
兩點.
(1)求![]() 的值;
的值;
(2)求出一次函數(shù)與反比例函數(shù)的表達式;
(3)過點![]() 作
作![]() 軸的垂線,與直線
軸的垂線,與直線![]() 和函數(shù)
和函數(shù)![]() (
(![]() )的圖象的交點分別為點
)的圖象的交點分別為點![]() ,
,![]() ,當(dāng)點
,當(dāng)點![]() 在點
在點![]() 下方時,寫出
下方時,寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
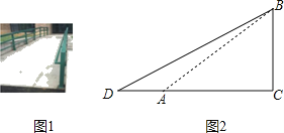
【題目】圖1是無障礙通道,圖2是其截面示意圖,已知坡角∠BAC=30°,斜坡AB=4m,∠ACB=90°.現(xiàn)要對坡面進行改造,使改造后的坡角∠BDC=26.5°,需要把水平寬度AC增加多少m(結(jié)果精確到0.1)?(參考數(shù)據(jù):![]() ≈1.73,sin26.5°≈0.45,cos26.5°≈0.90,tan26.5°≈0.50)
≈1.73,sin26.5°≈0.45,cos26.5°≈0.90,tan26.5°≈0.50)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
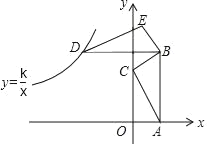
【題目】如圖,在平面直角坐標系中,△ABC的頂點A和C分別在x軸、y軸的正半軸上,且AB∥y軸,AB=4,△ABC的面積為2,將△ABC以點B為旋轉(zhuǎn)中心,順時針旋轉(zhuǎn)90°得到△DBE,一反比例函數(shù)圖象恰好過點D時,則此反比例函數(shù)解析式是_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
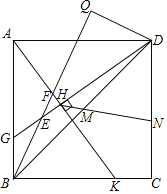
【題目】如圖,Q為正方形ABCD外一點,連接BQ,過點D作DQ⊥BQ,垂足為Q,G、K分別為AB、BC上的點,連接AK、DG,分別交BQ于F、E,AK⊥DG,垂足為點H,AF=5,DH=8,F為BQ中點,M為對角線BD的中點,連接HM并延長交正方形于點N,則HN的長為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在每個小正方形的邊長均為1的方格紙中有線段AB和CD,點A、B、C、D均在小正方形的頂點上.
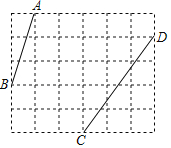
(1)畫出一個以AB為一邊的△ABE,點E在小正方形的頂點上,且∠BAE=45°,△ABE的面積為![]() ;
;
(2)畫出以CD為一腰的等腰△CDF,點F在小正方形的頂點上,且△CDF的面積為![]() ;
;
(3)在(1)、(2)的條件下,連接EF,請直接寫出線段EF的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】拋物線![]() 交
交![]() 軸于點
軸于點![]() ,
,![]() ,交
,交![]() 軸的負半軸于
軸的負半軸于![]() ,頂點為
,頂點為![]() .下列結(jié)論:①
.下列結(jié)論:①![]() ;②
;②![]() ;③當(dāng)
;③當(dāng)![]() 時,
時,![]() ;④當(dāng)
;④當(dāng)![]() 是等腰直角三角形時,則
是等腰直角三角形時,則![]() ;⑤若
;⑤若![]() ,
,![]() 是一元二次方程
是一元二次方程![]() 的兩個根,且
的兩個根,且![]() ,則
,則![]() .其中錯誤的有( )個.
.其中錯誤的有( )個.
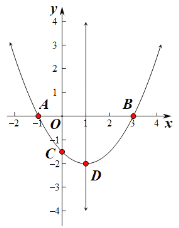
A.5B.4C.3D.2
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,![]() 是一張放在平面直角坐標系中的紙片,點
是一張放在平面直角坐標系中的紙片,點![]() 與原點
與原點![]() 重合,點
重合,點![]() 在
在![]() 軸的正半軸上,點
軸的正半軸上,點![]() 在
在![]() 軸的正半軸上.已知
軸的正半軸上.已知![]() ,
,![]() .將紙片的直角部分翻折,使點
.將紙片的直角部分翻折,使點![]() 落在
落在![]() 邊上,記為點
邊上,記為點![]() ,
,![]() 為折痕,點
為折痕,點![]() 在
在![]() 軸上.
軸上.

(1)在如圖所示的直角坐標系中,點![]() 的坐標為,________,
的坐標為,________,![]() ________;
________;
(2)線段![]() 上有一動點
上有一動點![]() (不與點
(不與點![]() ,
,![]() 重合)自點
重合)自點![]() 沿
沿![]() 方向以每秒
方向以每秒![]() 個單位長度向點
個單位長度向點![]() 做勻速運動,設(shè)運動時間為
做勻速運動,設(shè)運動時間為![]()
![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,求四邊形
,求四邊形![]() 的面積
的面積![]() 與時間
與時間![]() 之間的函數(shù)表達式.當(dāng)
之間的函數(shù)表達式.當(dāng)![]() 取何值時,
取何值時,![]() 有最大值?最大值是多少?
有最大值?最大值是多少?
(3)當(dāng)![]()
![]() 為何值時,
為何值時,![]() ,
,![]() ,
,![]() 三點構(gòu)成一個等腰三角形?并求出點
三點構(gòu)成一個等腰三角形?并求出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,AE是∠BAC的平分線,∠ABC的平分線 BM交AE于點M,點O在AB上,以點O為圓心,OB的長為半徑的圓經(jīng)過點M,交BC于點G,交 AB于點F.
(1)求證:AE為⊙O的切線.
(2)當(dāng)BC=8,AC=12時,求⊙O的半徑.
(3)在(2)的條件下,求線段BG的長.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com