
【題目】如圖, AB 是 ⊙ O 的直徑, C 是![]() 的中點, CE ⊥ AB 于 E , BD 交 CE 于 F .
的中點, CE ⊥ AB 于 E , BD 交 CE 于 F .
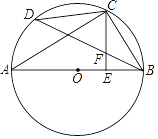
(1)求證: CF=BF ;
(2)若 CD=6 ,AC=8 ,求 BE 、 CF 的長.
【答案】(1)見解析;(2)3.6 ,![]()
【解析】
(1)延長CE交⊙O于點 P,根據垂徑定理得出及圓周角定理得出 ∠BCP=∠BDC ,又由C 是![]() 的中點,得∠BDC=∠CBD ,進而得出∠CBD=∠BCP ,從而得出結論;
的中點,得∠BDC=∠CBD ,進而得出∠CBD=∠BCP ,從而得出結論;
(2)根據圓周角定理及勾股定理得出 AB 的長,再由直角三角形相似,推出對應邊成比例,得出 BE 及 CE 的長,設 CF=x ,則 FE=4.8﹣x , BF=x ,根據勾股定理得出方程求解即可.
(1)證明:延長 CE 交 ⊙ O 于點 P ,
∵ CE ⊥ AB ,∴![]() ,
,
∴∠ BCP= ∠ BDC ,
∵ C 是![]() 的中點,
的中點,
∴ CD=CB ,
∴∠ BDC= ∠ CBD ,
∴∠ CBD= ∠ BCP ,
∴ CF=BF ;
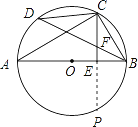
(2) ∵ CD=6 , AC=8 ,
∴ AB=10 ,
∵CF⊥AB,AC⊥BC, ∠CBA=∠EBC
∴△CBA∽△EBC
∴![]()
∴ BE= ![]() =3.6 ,
=3.6 ,
同理![]()
∴![]()
∴![]()
設 CF=x ,則 FE=4.8- x , BF=x ,
∵EF2+BE2=BF2
∴ (4.8﹣x)2 +3.62 =x2 ,
∴ x= ![]()
∴ CF=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】每年5月的第二個星期日即為母親節,“父母恩深重,恩憐無歇時”,許多市民喜歡在母親節為母親送花,感恩母親,祝福母親.今年節日前夕,某花店采購了一批鮮花禮盒,經分析上一年的銷售情況,發現該鮮花禮盒的該周銷售量y(盒)是銷售單價x(元)的一次函數,已知銷售單價為70元/盒時,銷售量為160盒;銷售單價為80元/盒時,銷售量為140盒.
(1)求該周銷售量y(盒)關于銷售單價x(元)的一次函數解析式;
(2)若按去年方式銷售,已知今年該鮮花禮盒的進價是每盒50元,商家要求該周至少要賣110盒,請你幫店長算一算,要完成商家的銷售任務,銷售單價不能超過多少元?
(3)在(2)的條件下,試確定銷售單價x為何值時,花店該周銷售鮮花禮盒獲得的利潤最大?并求出獲得的最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
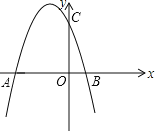
【題目】如圖,拋物線y=ax2+bx+3與x軸交于A(﹣3,0),B(l,0)兩點,與y軸交于點C.
(1)求拋物線的解析式;
(2)點P是拋物線上的動點,且滿足S△PAO=2S△PCO,求出P點的坐標;
(3)連接BC,點E是x軸一動點,點F是拋物線上一動點,若以B、C、E、F為頂點的四邊形是平行四邊形時,請直接寫出點F的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
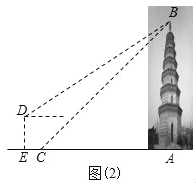
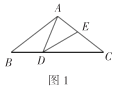
【題目】如圖(1),在豫西南鄧州市大十字街西南方,聳立著一座古老建筑-福勝寺梵塔,建于北宋天圣十年(公元1032年),學完了三角函數知識后,某校“數學社團”的劉明和王華決定用自己學到的知識測量“福勝寺梵塔”的高度.如圖(2),劉明在點C處測得塔頂B的仰角為45°,王華在高臺上的點D處測得塔頂B的仰角為40°,若高臺DE高為5米,點D到點C的水平距離EC為1.3米,且A、C、E三點共線,求該塔AB的高度.(參考數據:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,結果保留整數)

查看答案和解析>>
科目:初中數學 來源: 題型:
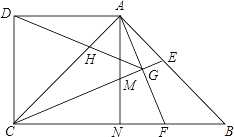
【題目】如圖,在四邊形 ABCD 中,AD ∥ BC ,∠BCD=90° ,∠ABC=45° ,AD=CD ,CE 平分 ∠ ACB 交 AB 于點 E ,在 BC 上截取 BF=AE ,連接 AF 交 CE 于點 G ,連接 DG 交 AC 于點 H ,過點 A 作 AN ⊥ BC ,垂足為 N , AN 交 CE 于點 M .則下列結論:① CM=AF ; ② CE ⊥ AF ; ③△ ABF ∽△ DAH ;④ GD 平分 ∠ AGC ,其中正確的序號是 ________ .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是
是![]() 邊上的一個動點(不與
邊上的一個動點(不與![]() ,
,![]() 重合),以
重合),以![]() 為邊作
為邊作![]() ,交
,交![]() 邊于點
邊于點![]() .設
.設![]() ,
,![]() .今天我們將根據學習函數的經驗,研究函數值
.今天我們將根據學習函數的經驗,研究函數值![]() 隨自變量
隨自變量![]() 的變化而變化的規律.
的變化而變化的規律.
下面是某同學做的一部分研究結果,請你一起參與解答:
(1)自變量![]() 的取值范圍是 ;
的取值范圍是 ;
(2)通過計算,得到![]() 與
與![]() 的幾組值,如下表:
的幾組值,如下表:
| 0.5 | 1 | 1.5 | 2 | 3 | 4 | 4.5 | 5 | 5.5 |
| 3.3125 | 2.75 | 2.3125 | 2 | 2.3125 | 2.75 | 3.3125 |
請你補全表格;
(3)在如圖2所示的平面直角坐標系中,畫出該函數的大致圖象;
(4)根據圖象,請寫出該函數的一條性質.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,將Rt△AOB繞點O順時針旋轉90°后得Rt△FOE,將線段EF繞點E逆時針旋轉90°后得線段ED,分別以O,E為圓心,OA、ED長為半徑畫弧AF和弧DF,連接AD,則圖中陰影部分面積是( )

A. π B. ![]() C. 3+π D. 8﹣π
C. 3+π D. 8﹣π
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l1:y=k1x+6與x軸、y軸分別交于A、B兩點,且OB=![]() OA,直線l2:y=k2x+b經過點C(
OA,直線l2:y=k2x+b經過點C(![]() ,1),與x軸、y軸、直線AB分別交于點E、F、D三點.
,1),與x軸、y軸、直線AB分別交于點E、F、D三點.
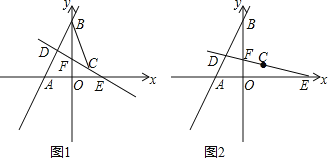
(1)求直線l1的解析式;
(2)如圖1,連接CB,當CD⊥AB時,求點D的坐標和△BCD的面積;
(3)如圖2,當點D在直線AB上運動時,在坐標軸上是否存在點Q,使△QCD是以CD為底邊的等腰直角三角形?若存在,請直接寫出點Q的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩車分別從A、B兩地同時出發,在同一條公路上,勻速行駛,相向而行,到兩車相遇時停止.甲車行駛一段時間后,因故停車0.5小時,故障解除后,繼續以原速向B地行駛,兩車之間的路程y(千米)與出發后所用時間x(小時)之間的函數關系如圖所示.

(1)求甲、乙兩車行駛的速度V甲、V乙.
(2)求m的值.
(3)若甲車沒有故障停車,求可以提前多長時間兩車相遇.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com