【題目】如圖，直線
與
軸、
軸分別相交于
、
兩點；分別過、兩點作軸、軸的垂線相交于
點.
為
邊上一動點．
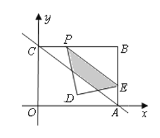
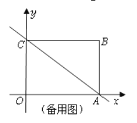
（1）求三角形
的面積；
（2）點從點出發沿著
以每秒1個單位長度的速度向點勻速運動，過點作
交
于
，設運動時間為
秒.用含的代數式表示
的面積
；
（3）在（2）的條件下點的運動過程中，將沿著
折疊（如圖所示），點在平面內的落點為點
．當
與
重疊部分的面積等于
時，試求出點的橫坐標．
【答案】（1）
的面積為24平方單位；（2）
；（3）當重疊部分的面積等于
時，
點的橫坐標為 
或6．
【解析】
（1）結合圖形，根據直線
與x軸、y軸分別相交于A、C兩點即可求出點C的坐標，故可求出面積；
（2）先證明四邊形OABC是矩形，根據性質得出BP的表達式，因為△BPE∽△BCA，求出BE表達式，進而求出△PBE的面積S．
（3）先求出D點在AC上的特殊位置時t的值，然后分兩種情況求解．
（1）令=0，解得x=8
∴A（8,0）
令x=0，y=6
∴C（0，6）
∴三角形
的面積=
OA×OC=×8×6=24平方單位
（2）與
軸相交于點
∵
，
，
∴四邊形
是矩形
∴
，
∴
∵
∴
∴
∴
∴
（3）設
、
與
分別相交于點
、
，得，
，
∵
∴
，
又∵
∴
∴
∴當點為
的中點時，
，點
恰好落在
上，
①當
時，
∵
∴
∴
∴
陰影
解得
，
（舍去）
∴點的橫坐標為，
②當
時，
解得
，
（舍去）
∴點的橫坐標為6
綜上所述：當重疊部分的面積等于時，點的橫坐標為 或6．
新思維小冠軍100分作業本系列答案
名師指導一卷通系列答案科目：初中數學 來源： 題型：
【題目】為了發展學生的核心素養，培養學生的綜合能力，某學校計劃開設四門選修課：樂器、舞蹈、繪畫、書法，學校采取隨機抽樣的方法進行問卷調查（每個被調查的學生必須選擇而且只能選擇其中一門）．對調查結果進行整理，繪制成如下兩幅不完整的統計圖．請結合圖中所給的信息解答下列問題：
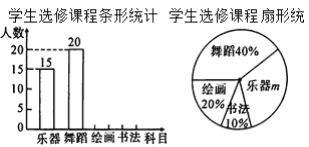
（1）本次調查的學生共有______人，在扇形統計圖中，m的值是______，將條形統計圖補充完整；
（2）在被調查的學生中，選修書法的有2名女同學，其余為男同學，現在要從中隨機抽取2名同學代表學校參加某社區組織的書法活動，請畫樹狀圖或列表求出所抽取的2名同學恰好是1名男同學和1名女同學的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】書籍是人類進步的階梯．聯合國教科文組織把每年的4月23日確定為“世界讀書日”．某校為了了解該校學生一個學期閱讀課外書籍的情況，在全校范圍內隨機對100名學生進行了問卷調查，根據調查的結果，繪制了統計圖表的一部分：一個學期平均一天閱讀課外書籍所有時間統計表
時間（分鐘） | 20 | 40 | 60 | 80 | 100 | 120 |
人數（名） | 43 | 31 | 15 | 5 | 4 | 2 |
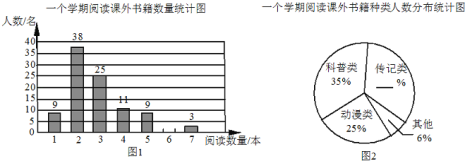
請你根據以上信息解答下列問題：
（1）補全圖1、圖2；
（2）這100名學生一個學期平均每人閱讀課外書籍多少本？若該校共有4000名學生，請你估計這個學校學生一個學期閱讀課外書籍共多少本？
（3）根據統計表，求一個學期平均一天閱讀課外書籍所用時間的眾數和中位數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】二次函數
的頂點
是直線
和直線
的交點．
(1)用含
的代數式表示頂點的坐標．
(2)①當
時，的值均隨
的增大而增大，求的取值范圍．
②若
，且滿足
時，二次函數的最小值為
，求
的取值范圍．
(3)試證明：無論取任何值，二次函數的圖象與直線總有兩個不同的交點．
查看答案和解析>>
科目：初中數學 來源： 題型：
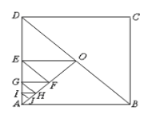
【題目】如圖，在邊長為1的正方形
中，當第1次作
，第2次作
；第3次作
，……依次方法繼續作垂直線段，當作到第10次時，所得的最小的三角形的面積是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC中，∠BAC=90°,AB=AC,點D在BC邊上，把△ABD沿AD折疊后，使得點B落在點E處，連接CE，若∠DBE=20°，則∠ADC=________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知二次函數
的圖象與
軸交于
、
兩點（點在點的左側），與
軸交于點
，且
，頂點為
．
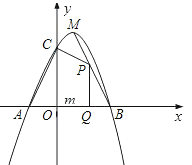
（1）求二次函數的解析式；
（2）點
為線段
上的一個動點，過點作軸的垂線
，垂足為
，若
，四邊形
的面積為
，求關于
的函數解析式，并寫出的取值范圍；
（3）探索：線段上是否存在點
，使
為等腰三角形？如果存在，求出點的坐標；如果不存在，請說呀理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
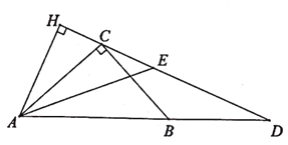
【題目】如釁，在Rt△ABC中，∠ACB=90°,sin∠BAC=
,點D在AB的延長線上，BD=BC,AE平分∠BAC交CD于點E，若AE=5
,則點A到直線CD的距離AH為________，BD的長為________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在四邊形ABCD中，AB∥DC，AB=AD，對角線AC．BD交于點O，AC平分∠BAD，過點C作CE⊥AB交AB的延長線于點E．連接OE．
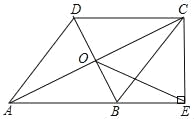
（1）求證：四邊形ABCD是菱形；
（2）若AB=
．OE=2，求線段CE的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com