
【題目】如圖,在平面直角坐標系![]() 中,直線
中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() 拋物線
拋物線![]() 的對稱軸是直線
的對稱軸是直線![]() 與
與![]() 軸的交點為點
軸的交點為點![]() 且經過點
且經過點![]() 兩點.
兩點.
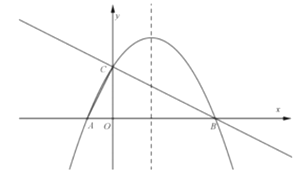
(1)求拋物線的解析式;
(2)點![]() 為拋物線對稱軸上一動點,當
為拋物線對稱軸上一動點,當![]() 的值最小時,請你求出點
的值最小時,請你求出點![]() 的坐標;
的坐標;
(3)拋物線上是否存在點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() 使得以點
使得以點![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?若存在,請直接寫出點
相似?若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在;
;(3)存在;![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)由直線![]() 可得B、C兩點的坐標,根據二次函數的對稱軸求得A點坐標,可設拋物線的解析式為
可得B、C兩點的坐標,根據二次函數的對稱軸求得A點坐標,可設拋物線的解析式為![]() ,將C點坐標代入可求得a,即可得拋物線的解析式;
,將C點坐標代入可求得a,即可得拋物線的解析式;
(2)根據絕對值的性質得出![]() 的值最小時,點
的值最小時,點![]() 為BC的垂直平分線與直線
為BC的垂直平分線與直線![]() 的交點,求得BC垂直平分線的解析式,聯立直線
的交點,求得BC垂直平分線的解析式,聯立直線![]() 即可求得點
即可求得點![]() ;
;
(3)分四種情況進行討論,設出N的坐標,根據相似三角形的對應邊成比例的性質,求得N的橫坐標與縱坐標的關系,然后聯立拋物線解析式即可求解.
解:∵直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,
,
∴當y=0時,即![]() ,解得:x=4,則點B的坐標為
,解得:x=4,則點B的坐標為![]() ,
,
當x=0時,![]() ,則點C的坐標為
,則點C的坐標為![]() ,
,
由二次函數的對稱性可知:點![]() 與點
與點![]() 關于直線
關于直線![]() 對稱,
對稱,
∴點A的坐標為![]() ,
,
∵拋物線與![]() 軸的交點為點
軸的交點為點![]() ,
,
∴可設拋物線的解析式為![]() ,
,
又∵拋物線過點![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
∴![]()
∴拋物線的解析式為![]() ;
;
(2)如圖1,連結CM、BM,作線段BC的垂直平分線![]() 分別交BC、直線
分別交BC、直線![]() 于點
于點![]() ,則N為BC中點;
,則N為BC中點;
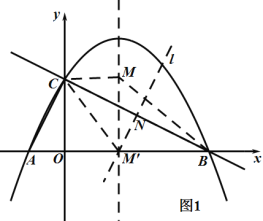
由絕對值的性質可得:![]() ,
,
∴當![]() 的值最小時,即
的值最小時,即![]() ,則此時
,則此時![]() ,
,
∴點M為![]() 與直線
與直線![]() 的交點,此時
的交點,此時![]() 與
與![]() 重合,
重合,
設![]() 的解析式為:
的解析式為:![]() ,
,
∵直線BC的解析式為:![]() ,
,![]()
∴![]() ,解得:
,解得:![]() ,則
,則![]() 的解析式可化為:
的解析式可化為:![]() ,
,
由![]() 得點N的坐標為
得點N的坐標為![]() ,
,
將![]() 代入
代入![]() 得:
得:
![]() ,解得:
,解得:![]() ,
,
∴![]() ,
,
將![]() 代入
代入![]() ,得
,得![]() ,即
,即![]() ,
,
∴當![]() 的值最小時,點
的值最小時,點![]() 的坐標為
的坐標為![]() ,
,
(3)拋物線上存在點![]() ,使得以點
,使得以點![]() 為頂點的三角形與
為頂點的三角形與![]() 相似;
相似;
∵![]()
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() 為直角三角形,
為直角三角形,![]() ,
,
∵![]() 軸,
軸,
∴![]() ,則
,則![]() ,
,
如圖2所示,分四種情況,點![]() 的坐標分別為
的坐標分別為![]() ,設點
,設點![]() 的坐標為
的坐標為![]() ,
,
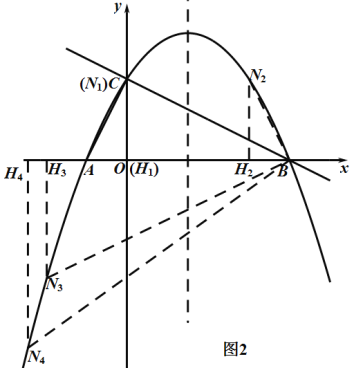
①當點![]() 在x軸的上方,要使
在x軸的上方,要使![]() ,則
,則![]() ,
,
則此時點![]() 與點C重合,則此時點
與點C重合,則此時點![]() 與點O重合,
與點O重合,
則![]() ,滿足題意,
,滿足題意,
∴此時點![]() 的坐標為
的坐標為![]() ;
;
②當點![]() 在x軸的上方,要使
在x軸的上方,要使![]() ,則
,則![]() ,
,
∴![]() ,即
,即![]() ,代入拋物線的解析式得:
,代入拋物線的解析式得:
![]() ,化簡得:
,化簡得:![]() ,
,
解得:![]() ,
,![]() (不符合題意,故舍去),
(不符合題意,故舍去),
將![]() 代入拋物線解析式得:
代入拋物線解析式得:![]() ,
,
∴此時點![]() 的坐標為
的坐標為![]() ;
;
③當點![]() 在x軸的下方,要使
在x軸的下方,要使![]() ,則
,則![]() ,
,
∴![]() ,即
,即![]() ,代入拋物線的解析式得:
,代入拋物線的解析式得:
![]() ,化簡得:
,化簡得:![]() ,
,
解得:![]() ,
,![]() (不符合題意,故舍去),
(不符合題意,故舍去),
將![]() 代入拋物線解析式得:
代入拋物線解析式得:![]() ,
,
∴此時點![]() 的坐標為
的坐標為![]() ;
;
④當點![]() 在x軸的下方,要使
在x軸的下方,要使![]() ,則
,則![]() ,
,
∴![]() ,即
,即![]() ,代入拋物線的解析式得:
,代入拋物線的解析式得:
![]() ,化簡得:
,化簡得:![]() ,
,
解得:![]() ,
,![]() (不符合題意,故舍去),
(不符合題意,故舍去),
將![]() 代入拋物線解析式得:
代入拋物線解析式得:![]() ,
,
∴此時點![]() 的坐標為
的坐標為![]() ;
;
綜上所述,拋物線存在點N的坐標為![]() 或
或![]() 或
或![]() 或
或![]() 使得以點
使得以點![]() 為頂點的三角形與
為頂點的三角形與![]() 相似.
相似.


科目:初中數學 來源: 題型:
【題目】2021年高考方案與高校招生政策都將有重大的變化,我市某部門為了了解政策的宣傳情況,對某初級中學學生進行了隨機抽樣調查,根據學生對政策的了解程度由高到低分為![]() ,
,![]() ,
,![]() ,
,![]() 四個等級,并對調查結果分析后繪制了如下兩幅不完整的統計圖,請你根據圖中提供的信息完成下列問題:
四個等級,并對調查結果分析后繪制了如下兩幅不完整的統計圖,請你根據圖中提供的信息完成下列問題:
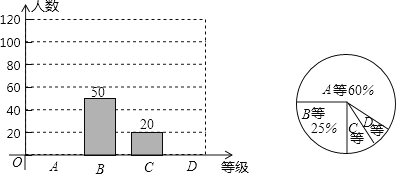
(1)求被調查學生的人數,并將條形統計圖補充完整;
(2)求扇形統計圖中的![]() 等對應的扇形圓心角的度數;
等對應的扇形圓心角的度數;
(3)已知該校有1500名學生,估計該校學生對政策內容了解程度為![]() 等的學生有多少人?
等的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=4,以AB為直徑的⊙O交BC于點D,交AC于點E,點P是AB的延長線上一點,且∠PDB=![]() ∠A,連接DE,OE.
∠A,連接DE,OE.
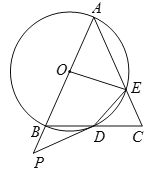
(1)求證:PD是⊙O的切線.
(2)填空:①當∠P的度數為______時,四邊形OBDE是菱形;
②當∠BAC=45°時,△CDE的面積為_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
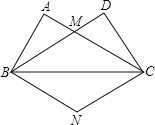
【題目】如圖,在△ABC和△DCB中,AB=DC,∠A=∠D,AC、DB交于點M.
(1)求證:△ABC≌△DCB;
(2)作CN∥BD,BN∥AC,CN交BN于點N,四邊形BNCM是什么四邊形?請證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,EF,EB是⊙O的弦,且EF=EB,EF與AB交于點C,連接OF,若∠AOF=40°,則∠F的度數是( )
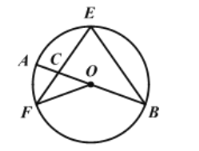
A.20°B.35°C.40°D.55°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校準備在各班設立圖書角以豐富同學們的課余文化生活.為了更合理的搭配各類書籍,學校團委以“我最喜愛的書籍”為主題,對學生最喜愛的一種書籍類型進行隨機抽樣調查,收集整理數據后,繪制出以下兩幅未完成的統計圖,請根據圖①和圖②提供的信息,解答下列問題:
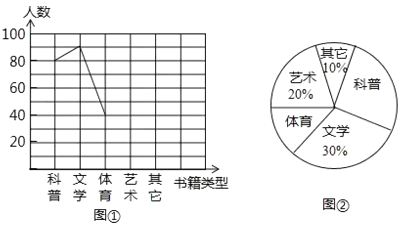
(1)在這次抽樣調查中,一共調查了_____________名學生;
(2)請把折線統計圖補充完整;
(3)在統計圖②中,求出“體育”部分所對應的圓心角的度數;
(4)若該校有學生2400人,估計喜歡“科普”書籍的有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為4,點E,F分別在邊AB,AD上,且∠ECF=45°,CF的延長線交BA的延長線于點G,CE的延長線交DA的延長線于點H,連接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)線段AC,AG,AH什么關系?請說明理由;
(3)設AE=m,
①△AGH的面積S有變化嗎?如果變化.請求出S與m的函數關系式;如果不變化,請求出定值.
②請直接寫出使△CGH是等腰三角形的m值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com