
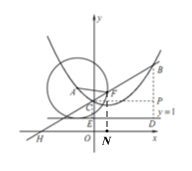
【題目】如圖,已知拋物線![]() 經過點
經過點![]() ,
,![]() .
.
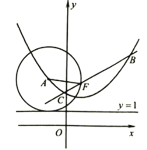
(1)求![]() 的值,并將拋物線解析式化成頂點式;
的值,并將拋物線解析式化成頂點式;
(2)已知點![]() ,點
,點![]() 為拋物線上一動點.求證:以
為拋物線上一動點.求證:以![]() 為圓心,
為圓心,![]() 為半徑的圓與直線
為半徑的圓與直線![]() 相切;
相切;
(3)在(2)的條件下,點![]() 為拋物線上一動點,作直線
為拋物線上一動點,作直線![]() ,與拋物線交于點
,與拋物線交于點![]() .當
.當![]() 時,請直接寫出直線
時,請直接寫出直線![]() 的解析式.
的解析式.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)證明見解析;(3)
;(2)證明見解析;(3)![]() 或
或![]() .
.
【解析】
(1)利用待定系數法可求出b、c的值,再將拋物線的解析式化為頂點式即可;
(2)如圖(見解析),由(1)可設點A的坐標為![]() ,再根據兩點之間的距離公式可得
,再根據兩點之間的距離公式可得![]() ,然后根據圓的切線的判定定理即可得證;
,然后根據圓的切線的判定定理即可得證;
(3)如圖(見解析),先根據正弦三角函數求出![]() ,從而可得
,從而可得![]() ,再利用正切三角函數可求出點H的坐標,然后利用待定系數法即可得;由根據二次函數的對稱性可得點B關于二次函數對稱軸的對稱點也滿足題設條件,利用同樣的方法求解即可得另一條符合要求的直線BF的解析式.
,再利用正切三角函數可求出點H的坐標,然后利用待定系數法即可得;由根據二次函數的對稱性可得點B關于二次函數對稱軸的對稱點也滿足題設條件,利用同樣的方法求解即可得另一條符合要求的直線BF的解析式.
(1)由題意,將點![]() ,
,![]() 代入拋物線解析式得:
代入拋物線解析式得: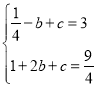
解得: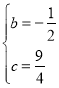
則![]() ;
;
(2)過點![]() 作
作![]() 垂直于直線
垂直于直線![]() ,垂足
,垂足![]()
設點A的坐標為![]()
則![]()
![]()
![]()
![]()
∴![]() ,即
,即![]()
∴![]() 是圓A的半徑
是圓A的半徑
∴以![]() 為圓心,
為圓心,![]() 為半徑的圓與直線
為半徑的圓與直線![]() 相切;
相切;
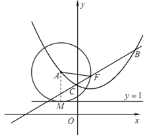
(3)如圖,過點![]() 、
、![]() 分別作直線
分別作直線![]() 的垂線,垂足分別為
的垂線,垂足分別為![]() 、
、![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,則四邊形CEDP是矩形
,則四邊形CEDP是矩形
![]() ,
,![]() 軸
軸
設![]() ,則
,則![]()
同(2)可得:![]() ,
,![]()
∴![]() ,
,![]()
在![]() 中,
中,![]()
∴![]()
設直線BF與x軸的交點為點![]() ,過點F作
,過點F作![]() 軸于點N
軸于點N
則點N的坐標為![]() ,
,![]() ,
,![]()
![]() 軸
軸
![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]() ,即點H的坐標為
,即點H的坐標為![]()
設直線BF的解析式為![]()
將點![]() 、
、![]() 代入得:
代入得: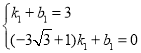 ,解得
,解得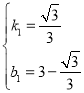
則此時直線![]() 的解析式為
的解析式為![]()
![]() 二次函數
二次函數![]() 的對稱軸為
的對稱軸為![]()
![]() 點
點![]() 在這個二次函數的對稱軸上
在這個二次函數的對稱軸上
則由二次函數的對稱性可知,圖中點B關于對稱軸為![]() 的對稱點也一定在拋物線上,且滿足
的對稱點也一定在拋物線上,且滿足![]()
同理可得:此時點H的坐標為![]()
設直線BF的解析式為![]()
將點![]() 、
、![]() 代入得:
代入得: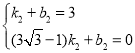 ,解得
,解得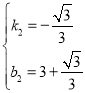
則此時直線![]() 的解析式為
的解析式為![]()
綜上,直線![]() 的解析式為
的解析式為![]() 或
或![]() .
.


 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:初中數學 來源: 題型:
【題目】“五一”期間,小明到小陳家所在的美麗鄉村游玩,在村頭A處小明接到小陳發來的定位,發現小陳家C在自己的北偏東45°方向,于是沿河邊筆直的綠道l步行200米到達B處,這時定位顯示小陳家C在自己的北偏東30°方向,如圖所示,根據以上信息和下面的對話,請你幫小明算一算他還需沿綠道繼續直走多少米才能到達橋頭D處(精確到1米)(備用數據:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年3月12日是第41個植樹節,某單位積極開展植樹活動,決定購買甲、乙兩種樹苗,用800元購買甲種樹苗的棵數與用680元購買乙種樹苗的棵數相同,乙種樹苗每棵比甲種樹苗每棵少6元.
(1)求甲種樹苗每棵多少元?
(2)若準備用3800元購買甲、乙兩種樹苗共100棵,則至少要購買乙種樹苗多少棵?
查看答案和解析>>
科目:初中數學 來源: 題型:
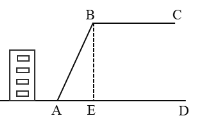
【題目】如圖,某校教學樓后面緊鄰著一個山坡,坡上面是一塊平地.![]() ,斜坡
,斜坡![]() 長
長![]() ,斜坡
,斜坡![]() 的坡比為12∶5.為了減緩坡面,防止山體滑坡,學校決定對該斜坡進行改造.經地質人員勘測,當坡角不超過50°時,可確保山體不滑坡.如果改造時保持坡腳A不動,則坡頂B沿
的坡比為12∶5.為了減緩坡面,防止山體滑坡,學校決定對該斜坡進行改造.經地質人員勘測,當坡角不超過50°時,可確保山體不滑坡.如果改造時保持坡腳A不動,則坡頂B沿![]() 至少向右移________
至少向右移________![]() 時,才能確保山體不滑坡.(取
時,才能確保山體不滑坡.(取![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一次函數![]() 的圖象與
的圖象與![]() 軸,
軸,![]() 軸分別交于A,C兩點,點B的坐標為
軸分別交于A,C兩點,點B的坐標為![]() ,二次函數
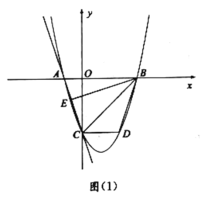
,二次函數![]() 的圖象過A,B,C三點,如圖(1).
的圖象過A,B,C三點,如圖(1).
(1)求二次函數的表達式;
(2)如圖(1),過點C作![]() 軸交拋物線于點D,點E在拋物線上(
軸交拋物線于點D,點E在拋物線上(![]() 軸左側),若
軸左側),若![]() 恰好平分
恰好平分![]() .求直線
.求直線![]() 的表達式;
的表達式;
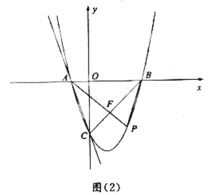
(3)如圖(2),若點P在拋物線上(點P在![]() 軸右側),連接
軸右側),連接![]() 交
交![]() 于點F,連接
于點F,連接![]() ,
,![]() .
.
①當![]() 時,求點P的坐標;
時,求點P的坐標;
②求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把正整數![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 排成如下的一個數表.
排成如下的一個數表.

(1)![]() 在第_____行,第______列;
在第_____行,第______列;
(2)第![]() 行第
行第![]() 列的數是_______(用含“
列的數是_______(用含“![]() ”的代數式表示)
”的代數式表示)
(3)嘉嘉和淇淇玩數學游戲,嘉嘉對淇淇說:“你從數表中挑一個數![]() ,按如圖所示的程序計算,只要你告訴我所得的數在第幾行,我就知道你挑的數在第幾行.”你認為嘉嘉說得有道理嗎?計算說明理由.
,按如圖所示的程序計算,只要你告訴我所得的數在第幾行,我就知道你挑的數在第幾行.”你認為嘉嘉說得有道理嗎?計算說明理由.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
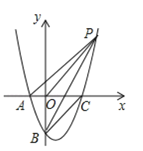
【題目】已知拋物線y=![]() x2+bx+c經過點A(﹣2,0)、B(0、﹣4)與x軸交于另一點C,連接BC.
x2+bx+c經過點A(﹣2,0)、B(0、﹣4)與x軸交于另一點C,連接BC.
(1)求拋物線的解析式.
(2)如圖,P是第一象限內拋物線上一點,且![]() ,求P點坐標.
,求P點坐標.
(3)在拋物線上是否存在點D,直線BD交x軸于點E,使![]() ABE與以A,B,C,E中的三點為頂點的三角形相似(不重合)?若存在,請求出點D的坐標;若不存在,請說明理由.
ABE與以A,B,C,E中的三點為頂點的三角形相似(不重合)?若存在,請求出點D的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com