
【題目】教材呈現:如圖是華師版九年級上冊數學教材第78頁的部分內容.
例2 如圖,在![]() 中,
中,![]() 分別是邊
分別是邊![]() 的中點,
的中點,![]() 相交于點
相交于點![]() ,求證:
,求證:![]() ,
,
證明:連結![]() .
.
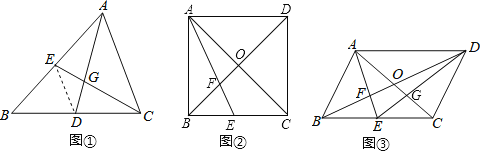
請根據教材提示,結合圖①,寫出完整的證明過程.
結論應用:在![]() 中,對角線
中,對角線![]() 交于點
交于點![]() ,
,![]() 為邊
為邊![]() 的中點,
的中點,![]() 、
、![]() 交于點
交于點![]() .
.
(1)如圖②,若![]() 為正方形,且
為正方形,且![]() ,則
,則![]() 的長為 .
的長為 .
(2)如圖③,連結![]() 交
交![]() 于點
于點![]() ,若四邊形
,若四邊形![]() 的面積為
的面積為![]() ,則
,則![]() 的面積為 .
的面積為 .
【答案】教材呈現:詳見解析;結論應用:(1)![]() ;(2)6.
;(2)6.
【解析】
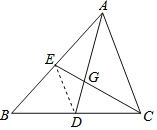
教材呈現:如圖①,連結![]() .根據三角形中位線定理可得
.根據三角形中位線定理可得![]() ,
,![]() ,那么
,那么![]() ,由相似三角形對應邊成比例以及比例的性質即可證明
,由相似三角形對應邊成比例以及比例的性質即可證明![]() ;
;
結論應用:(1)如圖②.先證明![]() ,得出
,得出![]() ,那么
,那么![]() ,又
,又![]() ,可得
,可得![]() ,由正方形的性質求出
,由正方形的性質求出![]() ,即可求出
,即可求出![]() ;
;
(2)如圖③,連接![]() .由(1)易證
.由(1)易證![]() .根據同高的兩個三角形面積之比等于底邊之比得出
.根據同高的兩個三角形面積之比等于底邊之比得出![]() 與
與![]() 的面積比
的面積比![]() ,同理,
,同理,![]() 與
與![]() 的面積比=2,那么
的面積比=2,那么![]() 的面積
的面積![]() 的面積=2(
的面積=2(![]() 的面積
的面積![]() 的面積)=
的面積)=![]() ,所以
,所以![]() 的面積
的面積![]() ,進而求出
,進而求出![]() 的面積
的面積![]() .
.
教材呈現:
證明:

如圖①,連結![]() .
.
∵在![]() 中,
中,![]() 分別是邊
分別是邊![]() 的中點,
的中點,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
結論應用:
(1)解:如圖②.
∵四邊形![]() 為正方形,
為正方形,![]() 為邊
為邊![]() 的中點,對角線
的中點,對角線![]() 、
、![]() 交于點
交于點![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵正方形![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案為![]() ;
;
(2)解:如圖③,連接![]() .
.
由(1)知,![]() ,
,
∴![]() .
.
∵![]() 與
與![]() 的高相同,
的高相同,
∴![]() 與
與![]() 的面積比
的面積比![]() ,
,
同理,![]() 與
與![]() 的面積比=2,
的面積比=2,
∴![]() 的面積
的面積![]() 的面積=2(
的面積=2(![]() 的面積
的面積![]() 的面積)
的面積)![]() ,
,
∴![]() 的面積
的面積![]() ,
,
∴![]() 的面積
的面積![]() .
.
故答案為6.


科目:初中數學 來源: 題型:
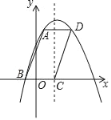
【題目】如圖,ABCD與拋物線y=﹣x2+bx+c相交于點A,B,D,點C在拋物線的對稱軸上,已知點B(﹣1,0),BC=4.
(1)求拋物線的解析式;
(2)求BD的函數表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx+3與x軸交于點A(﹣1,0),B(3,0).
(1)求拋物線的解析式;
(2)過點D(0,![]() )作x軸的平行線交拋物線于E,F兩點,求EF的長;
)作x軸的平行線交拋物線于E,F兩點,求EF的長;
(3)當y≤![]() 時,直接寫出x的取值范圍是 .
時,直接寫出x的取值范圍是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有甲,乙兩種機器人都被用來搬運某體育館室內裝潢材料甲型機器人比乙型機器人每小時少搬運30千克,甲型機器人搬運600千克所用的時間與乙型機器人搬運800千克所用的時間相同,兩種機器人每小時分別搬運多少千克?設甲型機器人每小時搬運x千克,根據題意,可列方程為( )
A. ![]() =
=![]() B.
B. ![]() =
=![]()
C. ![]() =
=![]() D.
D. ![]() =
=![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形![]() 中,
中,![]() 是
是![]() 中點,點
中點,點![]() 從點
從點![]() 出發(fā)沿
出發(fā)沿![]() 的路線勻速運動,到點
的路線勻速運動,到點![]() 停止,點
停止,點![]() 從點
從點![]() 出發(fā),沿
出發(fā),沿![]() 路線勻速運動,
路線勻速運動,![]() 、
、![]() 兩點同時出發(fā),點
兩點同時出發(fā),點![]() 的速度是點
的速度是點![]() 速度的
速度的![]() 倍
倍![]() ,當點
,當點![]() 停止時,點
停止時,點![]() 也同時停止運動,設
也同時停止運動,設![]() 秒時,正方形
秒時,正方形![]() 與
與![]() 重疊部分的面積為
重疊部分的面積為![]() ,
,![]() 關于
關于![]() 的函數關系如圖2所示,則
的函數關系如圖2所示,則
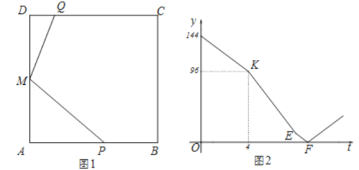
(1)求正方形邊長![]() ;
;
(2)求![]() 的值;
的值;
(3)求圖2中線段![]() 所在直線的解析式.
所在直線的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,根據圖象解答下列問題:
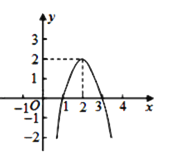
(1)寫出方程ax2+bx+c=0的兩個根;
(2)寫出y隨x的增大而減小的自變量x的取值范圍;
(3)若方程ax2+bx+c=k有兩個不相等的實數根,求k的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c的圖象與x軸交于點A(﹣1,0),與y軸的交點B在(0,2)與(0,3)之間(不包括這兩點),對稱軸為直線x=2.下列結論:abc<0;②9a+3b+c>0;③若點M(![]() ,y1),點N(
,y1),點N(![]() ,y2)是函數圖象上的兩點,則y1<y2;④﹣
,y2)是函數圖象上的兩點,則y1<y2;④﹣![]() <a<﹣
<a<﹣![]() .其中正確結論有( )
.其中正確結論有( )
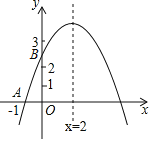
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形 ACDE 是證明勾股定理時用到的一個圖形,a 、b 、c 是 RtABC和 RtBED 的邊長,已知![]() ,這時我們把關于 x 的形如
,這時我們把關于 x 的形如![]() 二次方程稱為“勾系一元二次方程”.
二次方程稱為“勾系一元二次方程”.

請解決下列問題:
(1)寫出一個“勾系一元二次方程”;
(2)求證:關于 x 的“勾系一元二次方程”![]() ,必有實數根;
,必有實數根;
(3)若 x 1是“勾系一元二次方程” ![]() 的一個根,且四邊形 ACDE 的周長是6
的一個根,且四邊形 ACDE 的周長是6![]() ,求ABC 的面積.
,求ABC 的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
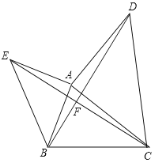
【題目】如圖,已知△ABC,分別以AB,AC為直角邊,向外作等腰直角三角形ABE和等腰直角三角形ACD,∠EAB=∠DAC=90°,連結BD,CE交于點F,設AB=m,BC=n.下列結論①∠BDA=∠ECA; ②若m=![]() ,n=3,∠ABC=75°,則BD=
,n=3,∠ABC=75°,則BD=![]() ;③當∠ABC=135°時,BD最大,最大值為
;③當∠ABC=135°時,BD最大,最大值為![]() m+n;④AE2=BF2+EF2中正確的有_______。
m+n;④AE2=BF2+EF2中正確的有_______。
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com