
【題目】如圖,在![]() ABC中,AB=BC,以△ABC的邊AB為直徑作⊙O,交AC于點D,過點D作DE⊥BC,垂足為點E.
ABC中,AB=BC,以△ABC的邊AB為直徑作⊙O,交AC于點D,過點D作DE⊥BC,垂足為點E.
(1)試證明DE是⊙O的切線;
(2)若⊙O的半徑為5,AC=6![]() ,求此時DE的長.
,求此時DE的長.

【答案】(1)見解析;(2)3
【解析】
(1)連接OD、BD,求出BD⊥AD,AD=DC,根據三角形的中位線得出OD∥BC,推出OD⊥DE,根據切線的判定推出即可;
(2)先利用勾股定理求出BD的長,證得Rt△CDE和Rt△ABD,利用對應邊成比例即可求解.
(1)證明:連接OD,BD,

∵AB為⊙O的直徑,
∴BD⊥AD,
又∵AB=BC,△ABC是等腰三角形,
∴AD=DC,
∴OD是△ABC的中位線,
∴OD∥BC,
又DE⊥BC,
∴DE⊥OD,
∴DE是⊙O的切線;
(2)由(1)知,BD是AC邊上的中線,AC=6![]() ,
,
得AD=CD=3![]() ,
,
∵⊙O的半徑為5,
∴AB=10,
在Rt△ABD中,BD=![]() ,
,
∵AB=BC,
∴∠A=∠C,
在Rt△CDE和Rt△ABD中,
∵∠DEC=∠ADB=90°,∠C=∠A,
∴Rt△CDE∽Rt△ABD,
∴![]() ,即
,即![]() ,
,
解得:DE=3.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 為斜邊
為斜邊![]() 的中線,過點D作
的中線,過點D作![]() 于點E,延長
于點E,延長![]() 至點F,使
至點F,使![]() ,連接
,連接![]() ,點G在線段
,點G在線段![]() 上,連接
上,連接![]() ,且
,且![]() .下列結論:①
.下列結論:①![]() ;②四邊形
;②四邊形![]() 是平行四邊形;③
是平行四邊形;③![]() ;④
;④![]() .其中正確結論的個數是( )
.其中正確結論的個數是( )
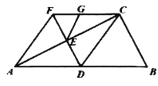
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線![]() 與兩條坐標軸分別交于
與兩條坐標軸分別交于![]() ,
,![]() ,
,![]() 三點.其中
三點.其中![]() ,且
,且![]() .
.
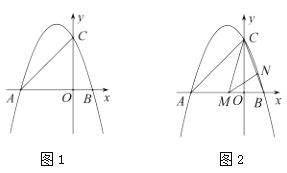
(1)求該拋物線的解析式;
(2)點![]() 是
是![]() 軸上一點,拋物線上是否存在點
軸上一點,拋物線上是否存在點![]() ,使得以點
,使得以點![]() ,
,![]() ,
,![]() ,
,![]() 為頂點,以
為頂點,以![]() 為邊的四邊形是平行四邊形?若存在,求出點
為邊的四邊形是平行四邊形?若存在,求出點![]() 的坐標;若不存在,請說明理由;
的坐標;若不存在,請說明理由;
(3)如圖2,點![]() ,
,![]() 分別是線段
分別是線段![]() ,
,![]() 上的動點,連接
上的動點,連接![]() ,
,![]() ,當
,當![]() 時,求點
時,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點![]() 在
在![]() 上.則下列命題為真命題的是( )
上.則下列命題為真命題的是( )
A.若半徑![]() 平分弦
平分弦![]() .則四邊形
.則四邊形![]() 是平行四邊形
是平行四邊形
B.若四邊形![]() 是平行四邊形.則
是平行四邊形.則![]()
C.若![]() .則弦
.則弦![]() 平分半徑
平分半徑![]()
D.若弦![]() 平分半徑
平分半徑![]() .則半徑
.則半徑![]() 平分弦
平分弦![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
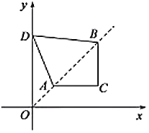
【題目】如圖,在直角坐標系中,點![]() ,
,![]() 是第一象限角平分線上的兩點,點
是第一象限角平分線上的兩點,點![]() 的縱坐標為1,且
的縱坐標為1,且![]() ,在
,在![]() 軸上取一點
軸上取一點![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,
,![]() ,使得四邊形
,使得四邊形![]() 的周長最小,這個最小周長的值為________.
的周長最小,這個最小周長的值為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
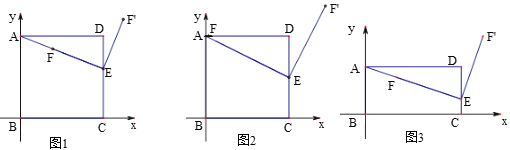
【題目】正方形ABCD的邊長為4,以B為原點建立如圖1平面直角坐標系中,E是邊CD上的一個動點,F是線段AE上一點,將線段EF繞點E順時針旋轉90°得到EF'.
(1)如圖2,當E是CD中點,![]() 時,求點F'的坐標.
時,求點F'的坐標.
(2)如圖1,若![]() ,且F',D,B在同一直線上時,求DE的長.
,且F',D,B在同一直線上時,求DE的長.
(3)如圖3,將正邊形ABCD改為矩形,AD=4,AB=2,其他條件不變,若![]() ,且F',D,B在同一直線上時,則DE的長是_______.(請用含n的代數式表示)
,且F',D,B在同一直線上時,則DE的長是_______.(請用含n的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
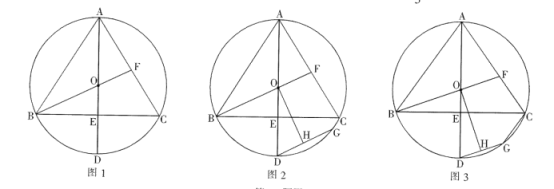
【題目】已知![]() 是
是![]() 的外接圓,AD為
的外接圓,AD為![]() 的直徑,
的直徑,![]() ,垂足為E,連接BO,延長BO交AC于點F.
,垂足為E,連接BO,延長BO交AC于點F.
(1)如圖1,求證:![]() ;
;
(2)如圖2,過點D作![]() ,交
,交![]() 于點G,點H為GD的中點,連接OH,求證:
于點G,點H為GD的中點,連接OH,求證:![]() ;
;
(3)如圖3,在(2)的條件下,連接CG,若![]() 的面積為
的面積為![]() ,求線段CG的長.
,求線段CG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,函數y=![]() (x>0)的圖象與直線y=mx交于點A(2,2).
(x>0)的圖象與直線y=mx交于點A(2,2).
(1)求k,m的值;
(2)點P的橫坐標為n(n>0),且在直線y=mx上,過點P作平行于x軸的直線,交y軸于點M,交函數y=![]() (x>0)的圖象于點N.
(x>0)的圖象于點N.
①n=1時,用等式表示線段PM與PN的數量關系,并說明理由;
②若PN≥3PM,結合函數的圖象,直接寫出n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某數學活動小組在作三角形的拓展圖形,研究其性質時,經歷了如下過程:
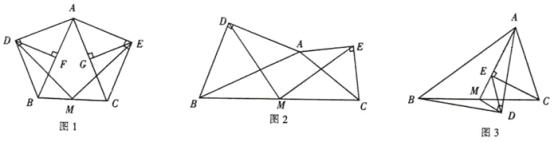
●操作發現:
在等腰△ABC中,AB=AC,分別以AB和AC為斜邊,向△ABC的外側作等腰直角三角形,如圖1所示,其中DF⊥AB于點F,EG⊥AC于點G,M是BC的中點,連接MD和ME,則下列結論正確的是 (填序號即可)
①AF=AG=![]() AB;②MD=ME;③整個圖形是軸對稱圖形;④∠DAB=∠DMB.
AB;②MD=ME;③整個圖形是軸對稱圖形;④∠DAB=∠DMB.
●數學思考:
在任意△ABC中,分別以AB和AC為斜邊,向△ABC的外側作等腰直角三角形,如圖2所示,M是BC的中點,連接MD和ME,則MD和ME具有怎樣的數量和位置關系?請給出證明過程;
●類比探索:
在任意△ABC中,仍分別以AB和AC為斜邊,向△ABC的內側作等腰直角三角形,如圖3所示,M是BC的中點,連接MD和ME,試判斷△MED的形狀.
答: .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com