
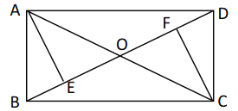
【題目】如圖,矩形![]() 的對角線
的對角線![]() 、
、![]() 相交于點
相交于點![]() ,點
,點![]() 、
、![]() 在
在![]() 上,
上,![]() .
.
(1)求證:![]() ;
;
(2)若![]() ,
,![]() ,求矩形
,求矩形![]() 的面積.
的面積.
【答案】(1)見解析;(2)![]() .
.
【解析】
(1)由矩形的性質得出OA=OC,OB=OD,AC=BD,∠ABC=90°,證出OE=OF,由SAS證明△AOE≌△COF,即可得出AE=CF;
(2)證出△AOB是等邊三角形,得出OA=AB=6,AC=2OA=12,在Rt△ABC中,由勾股定理求出BC=![]() =6
=6![]() ,即可得出矩形ABCD的面積.
,即可得出矩形ABCD的面積.
(1)證明:∵四邊形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,∠ABC=90°,
∵BE=DF,
∴OE=OF,
在△AOE和△COF中,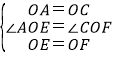 ,
,
∴△AOE≌△COF(SAS),
∴AE=CF;
(2)∵OA=OC,OB=OD,AC=BD,
∴OA=OB,
∵∠AOB=∠COD=60°,
∴△AOB是等邊三角形,
∴OA=AB=6,
∴AC=2OA=12,
在Rt△ABC中,BC=![]() ,
,
∴矩形ABCD的面積=ABBC=6×6![]() =36
=36![]() .
.


 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標平面上,△AOB是直角三角形,點O在原點上,A、B兩點的坐標分別為(-1,y1)、(3,y2),線段AB交y軸于點C.若S△AOC=1,記∠AOC為α,∠BOC為β,則sin α·sin β的值為____.

查看答案和解析>>
科目:初中數學 來源: 題型:
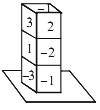
【題目】如圖,將3個同樣的正方體重疊放置在桌面上,每個正方體的6個面上分別寫有-3、-2、-1、1、2、3,相對的兩面上寫的數字互為相反數,現在有5個面的數字無論從哪個角度都看不到,這5個看不到的面上數字的乘積是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
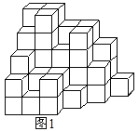
【題目】如圖1,是一個由53個大小相同的小正方體堆成的立體圖形,從正面觀察這個立體圖形得到的平面圖形如圖2所示.
(1)請在圖3、圖4中依次畫出從左面、上面觀察這個立體圖形得到的平面圖形
(2)保持這個立體圖形中最底層的小正方體不動,從其余部分中取走k個小正方體,得到一個新的立體圖形.如果依次從正面、左面、上面觀察新的立體圖形,所得到的平面圖形分別與圖2、圖3、圖4是一樣的,那么k的最大值為 .



查看答案和解析>>
科目:初中數學 來源: 題型:
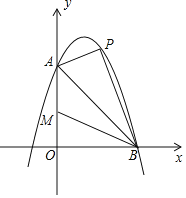
【題目】如圖,已知拋物線![]() 與y軸交于點
與y軸交于點![]() ,與x軸交于點
,與x軸交于點![]() ,點P是線段AB上方拋物線上的一個動點.
,點P是線段AB上方拋物線上的一個動點.
![]() 求這條拋物線的表達式及其頂點坐標;
求這條拋物線的表達式及其頂點坐標;
![]() 當點P移動到拋物線的什么位置時,使得
當點P移動到拋物線的什么位置時,使得![]() ,求出此時點P的坐標;
,求出此時點P的坐標;
![]() 當點P從A點出發沿線段AB上方的拋物線向終點B移動,在移動中,點P的橫坐標以每秒1個單位長度的速度變動;與此同時點M以每秒1個單位長度的速度沿AO向終點O移動,點P,M移動到各自終點時停止
當點P從A點出發沿線段AB上方的拋物線向終點B移動,在移動中,點P的橫坐標以每秒1個單位長度的速度變動;與此同時點M以每秒1個單位長度的速度沿AO向終點O移動,點P,M移動到各自終點時停止![]() 當兩個動點移動t秒時,求四邊形PAMB的面積S關于t的函數表達式,并求t為何值時,S有最大值,最大值是多少?
當兩個動點移動t秒時,求四邊形PAMB的面積S關于t的函數表達式,并求t為何值時,S有最大值,最大值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
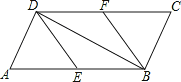
【題目】如圖,在平行四邊形ABCD中,E、F分別為邊AB、CD的中點,BD是對角線.
(1)求證:△ADE≌△CBF;
(2)若∠ADB是直角,則四邊形BEDF是什么四邊形?證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為打造書香校園,計劃購進甲、乙兩種規格的書柜放置新購進的圖書,調查發現,若購買甲種書柜3個、乙種書柜2個,共需資金1020元;若購買甲種書柜4個,乙種書柜3個,共需資金1440元.
(1)甲、乙兩種書柜每個的價格分別是多少元?
(2)若該校計劃購進這兩種規格的書柜共20個,其中乙種書柜的數量不少于甲種書柜的數量,學校至多能夠提供資金4320元,請設計幾種購買方案供這個學校選擇.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某汽車出發前油箱內有油42L,行駛若干小時后,在途中加油站加油若干升.郵箱中剩余油量Q(L)與行駛時間t(h)之間的函數關系如圖所示.
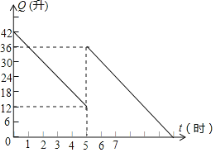
(1)汽車行駛 h后加油,加油量為 L;
(2)求加油前油箱剩余油量Q與行駛時間t之間的函數關系式;
(3)如果加油站離目的地還有200km,車速為40km/h,請直接寫出汽車到達目的地時,油箱中還有多少汽油?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀思考
我們知道,在數軸上|a|表示數a所對應的點到原點的距離,這是絕對值的幾何意義,由此我們可進一步地來研究數軸上任意兩個點之間的距離,一般地,如果數軸上兩點A、B 對立的數用a,b表示,那么這兩個點之間的距離AB=|a﹣b|.也可以用兩點中右邊的點所表示數的減去左邊的點所表示的數來計算,例如:數軸上P,Q兩點表示的數分別是﹣1和2,那么P,Q兩點之間的距離就是 PQ=2﹣(﹣1)=3.
啟發應用
如圖,點A在數軸上對應的數為a,點B對應的數為b,且a、b滿足|a+3|+(b﹣2)2=0
(1)求線段AB的長;
(2)如圖,點C在數軸上對應的數為x,且x是方程2x+1=![]() x﹣8的解,
x﹣8的解,
①求線段BC的長;
②在數軸上是否存在點P使PA+PB=BC?若存在,直接寫出點P對應的數:若不存在,說明理由.
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com