
【題目】如圖,已知A,B,C,D為矩形的四個頂點(diǎn),AB=16 cm,AD=6 cm,動點(diǎn)P,Q分別從點(diǎn)A,C同時出發(fā),點(diǎn)P以3 cm/s的速度向點(diǎn)B移動,一直到點(diǎn)B為止,點(diǎn)Q以2 cm/s的速度向點(diǎn)D移動,當(dāng)點(diǎn)P停止運(yùn)動時,點(diǎn)Q也停止運(yùn)動.問:
(1)P,Q兩點(diǎn)從開始出發(fā)多長時間時,四邊形PBCQ的面積是33 cm2?
(2)P,Q兩點(diǎn)從開始出發(fā)多長時間時,點(diǎn)P與點(diǎn)Q之間的距離是10 cm?

【答案】(1) P,Q兩點(diǎn)從開始出發(fā)5s時,四邊形PBCQ的面積是33cm2;(2) P,Q兩點(diǎn)從開始出發(fā)1.6s或4.8s時,點(diǎn)P與點(diǎn)Q之間的距離是10cm.
【解析】試題分析:(1)、首先設(shè)xs時面積為33,然后根據(jù)梯形的面積計算法則列出方程,從而求出答案;(2)、過點(diǎn)Q作QH⊥AB于H,然后求出PH的長度,最后根據(jù)Rt△PHQ的勾股定理求出未知數(shù)的值得出答案.
試題解析:解:(1)設(shè)P,Q兩點(diǎn)從開始出發(fā)xs時,四邊形PBCQ的面積是33cm2.
則由題意得![]() ×(16-3x+2x)×6=33,
×(16-3x+2x)×6=33,
解得x=5.(3分)∵16÷3=![]() >5,
>5,
∴x=5符合題意.
故P,Q兩點(diǎn)從開始出發(fā)5s時,四邊形PBCQ的面積是33cm2;
(2)設(shè)P,Q兩點(diǎn)從開始出發(fā)ys時,點(diǎn)P與Q之間的距離是10cm,
過點(diǎn)Q作QH⊥AB于H,
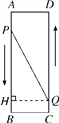
∴∠QHA=90°.∵四邊形ABCD是矩形,∴∠A=∠D=90°,
∴四邊形ADQH是矩形,∴AH=DQ=(16-2y)cm,QH=AD=6cm,
∴當(dāng)P點(diǎn)在H點(diǎn)上方時,PH=AH-AP=16-2y-3y=(16-5y)(cm);當(dāng)P點(diǎn)在H點(diǎn)下方時,PH=AP-AH=3y-(16-2y)=(5y-16)(cm), ∴PH=|16-5y|cm.
在Rt△PQH中,根據(jù)勾股定理得PH2+QH2=PQ2,
即(16-5y)2+62=102,解得y1=1.6,y2=4.8. ∵16÷3=![]() ,
,
∴y1=1.6和y2=4.8均符合題意.
故P,Q兩點(diǎn)從開始出發(fā)1.6s或4.8s時,點(diǎn)P與點(diǎn)Q之間的距離是10cm.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,△ABC的位置如圖所示(每個小方格都是邊長為1個單位長度的正方形).
(1)將△ABC沿x軸方向向左平移6個單位,畫出平移后得到的△A1B1C1;
(2)將△ABC繞著點(diǎn)A順時針旋轉(zhuǎn)90°,畫出旋轉(zhuǎn)后得到的△AB2C2,并直接寫出點(diǎn)B2、C2的坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,D為⊙O上一點(diǎn),點(diǎn)C在直徑BA的延長線上,且∠CDA=∠CBD.
(1)求證:CD是⊙O的切線;
(2)過點(diǎn)B作⊙O的切線交CD的延長線于點(diǎn)E,CD=2![]() .
.
①若∠C=30°,求圖中陰影部分的面積;
②若![]() ,求BE的長.
,求BE的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小明某天上午9時騎自行車離開家,15時回家,他離家的距離與時間的變化情況如圖所示.

(1)10時時他離家 ![]() ,他到達(dá)離家最遠(yuǎn)的地方時是 時,此時離家
,他到達(dá)離家最遠(yuǎn)的地方時是 時,此時離家 ![]() ;
;
(2)他可能在哪段時間內(nèi)休息,并吃午餐?
(3)他在出行途中,哪段時間內(nèi)騎車速度最快,速度是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)![]() .
.
(1)證明:不論![]() 取何值,該函數(shù)圖像與
取何值,該函數(shù)圖像與![]() 軸總有公共點(diǎn);
軸總有公共點(diǎn);
(2)若該函數(shù)的圖像與![]() 軸交于點(diǎn)(0,3),求出頂點(diǎn)坐標(biāo)并畫出該函數(shù)圖像;
軸交于點(diǎn)(0,3),求出頂點(diǎn)坐標(biāo)并畫出該函數(shù)圖像;
(3)在(2)的條件下,觀察圖像,解答下列問題:
①不等式![]() 的的解集是 ;
的的解集是 ;
②若一元二次方程![]() 有兩個不相等的實(shí)數(shù)根,則
有兩個不相等的實(shí)數(shù)根,則![]() 的取值范圍是 ;
的取值范圍是 ;
③若一元二次方程![]() 在
在![]() 的范圍內(nèi)有實(shí)數(shù)根,則
的范圍內(nèi)有實(shí)數(shù)根,則![]() 的取
的取
值范圍是 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
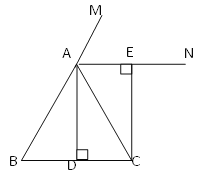
【題目】如圖所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足為D,AN是△ABC外角∠CAM的平分線,CE⊥AN,垂足為E.
(1)求證:四邊形ADCE是矩形;
(2)當(dāng)△ABC滿足什么條件時,四邊形ADCE是正方形?給出證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小紅家春天粉刷房間,雇用了5個工人,做了10天完工。用了某種涂料150升,費(fèi)用為4800元;粉刷的面積為150![]() 。最后結(jié)算工錢時有以下幾種方案:
。最后結(jié)算工錢時有以下幾種方案:
方案1:按工算,每個工30元;(1個工人做一天是一個工)
方案2:按涂料費(fèi)用算,涂料費(fèi)用的30%作為工錢;
方案3:按粉刷面積算,每平方米付工錢12元。
請你幫小紅家出主意,選擇那種方案付錢最合算?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某種子商店銷售“黃金一號”玉米種子,為惠民促銷,推出兩種銷售方案供采購者選擇.
方案一:每千克種子價格為4元,均不打折;
方案二:購買3千克以內(nèi)(含3千克)的價格為每千克5元,若一次購買超過3千克,則超出部分的種子打七折.
(1)請分別求出方案一、方案二中購買的種子數(shù)量x(千克)與付款金額y(元)之間的函數(shù)關(guān)系式;
(2)若你去購買一定量的種子,你會怎樣選擇方案?說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com