【題目】火鍋是重慶的一張名片，深受廣大市民的喜愛.重慶某火鍋店采取堂食、外賣、店外擺攤（簡稱擺攤）三種方式經(jīng)營，6月份該火鍋店堂食、外賣、擺攤三種方式的營業(yè)額之比為3：5：2．隨著促進消費政策的出臺，該火鍋店老板預計7月份總營業(yè)額會增加，其中擺攤增加的營業(yè)額占總增加的營業(yè)額的
，則擺攤的營業(yè)額將達到7月份總營業(yè)額的
，為使堂食、外賣7月份的營業(yè)額之比為8：5，則7月份外賣還需增加的營業(yè)額與7月份總營業(yè)額之比是__________．
【答案】
【解析】
先根據(jù)題意設出相應的未知數(shù)，再結合題目的等量關系列出相應的方程組，最后求解即可求得答案．
解：設6月份該火鍋店堂食、外賣、擺攤三種方式的營業(yè)額分別為3k，5k，2k，7月份總增加的營業(yè)額為m，則7月份擺攤增加的營業(yè)額為
m，設7月份外賣還需增加的營業(yè)額為x．
∵7月份擺攤的營業(yè)額是總營業(yè)額的
，且7月份的堂食、外賣營業(yè)額之比為8：5，
∴7月份的堂食、外賣、擺攤三種方式的營業(yè)額之比為8：5：7，
∴設7月份的堂食、外賣、擺攤三種方式的營業(yè)額分別為8a，5a，7a，
由題意可知：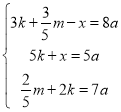
，
解得：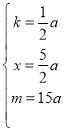
，
∴
，
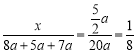故答案為：．
科目：初中數(shù)學 來源： 題型：
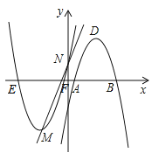
【題目】如圖，直線
交
軸于點A，交
軸于點B,拋物線
經(jīng)過點A，交軸于點
，點P為直線AB下方拋物線上一動點，過點P作
于D，連接AP．
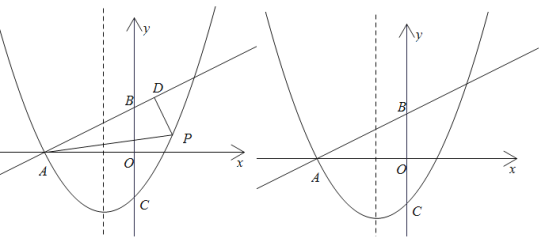
（1）求拋物線的解析式；
（2）若以點
為頂點的三角形與
相似，求點P的坐標；
（3）將繞點A旋轉，當點O的對應點
落在拋物線的對稱軸上時，請直接寫出點B的對應點
的坐標．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，在平面直角坐標系中，已知拋物線
：
的頂點為
，與
軸相交于點
，先將拋物線沿
軸翻折，再向右平移p個單位長度后得到拋物
，直線
；
經(jīng)過，兩點．
（1）求點的坐標，并結合圖象直接寫出不等式：
的解集；
（2）若拋物線的頂點
與點關于原點對稱，求p的值及拋物線的解析式；
（3）若拋物線與軸的交點為
、
（點、分別與拋物線上點
、
對應），試問四邊形
是何種特殊四邊形？并說明其理由．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】疫情防控，我們一直在堅守．某居委會組織兩個檢查組，分別對“居民體溫”和“居民安全出行”的情況進行抽查．若這兩個檢查組在轄區(qū)內的某三個校區(qū)中各自隨機抽取一個小區(qū)進行檢查，則他們恰好抽到同一個小區(qū)的概率是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
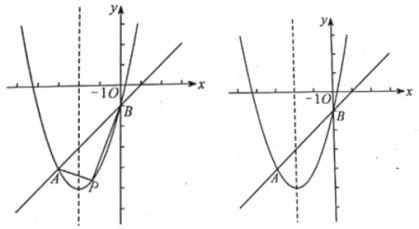
【題目】如圖，在平面直角坐標系中，已知拋物線
與直線AB相交于A，B兩點，其中
，
．
（1）求該拋物線的函數(shù)表達式；
（2）點P為直線AB下方拋物線上的任意一點，連接PA，PB，求
面積的最大值；
（3）將該拋物線向右平移2個單位長度得到拋物線
，平移后的拋物線與原拋物線相交于點C，點D為原拋物線對稱軸上的一點，在平面直角坐標系中是否存在點E，使以點B，C，D，E為頂點的四邊形為菱形，若存在，請直接寫出點E的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，在梯形
中，
，
，
，
．P為線段
上的一動點，且和B、C不重合，連接
，過點P作
交射線
于點E．
聰聰根據(jù)學習函數(shù)的經(jīng)驗，對這個問題進行了研究：
（1）通過推理，他發(fā)現(xiàn)
，請你幫他完成證明．
（2）利用幾何畫板，他改變的長度，運動點P，得到不同位置時，
、
的長度的對應值：
當
時，得表1：
| … | 1 | 2 | 3 | 4 | 5 | … |
| … | 0.83 | 1.33 | 1.50 | 1.33 | 0.83 | … |
當
時，得表2：
| … | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| … | 1.17 | 2.00 | 2.50 | 2.67 | 2.50 | 2.00 | 1.17 | … |
這說明，點P在線段上運動時，要保證點E總在線段上，
的長度應有一定的限制．
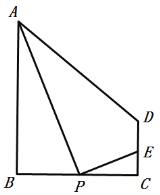
①填空：根據(jù)函數(shù)的定義，我們可以確定，在和的長度這兩個變量中，_____的長度為自變量，_____的長度為因變量；
②設
，當點P在線段上運動時，點E總在線段上，求m的取值范圍．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
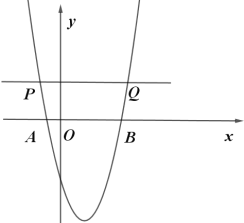
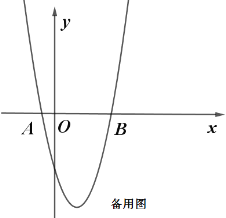
【題目】如圖，已知二次函數(shù)y＝ax2＋bx－5（a，b是常數(shù)，a
0）的圖象與x軸交于點A（－1，0）和點B（5，0）．動直線y＝t（t為常數(shù)）與拋物線交于不同的兩點P、Q（點P在Q的左側）．
（1）求拋物線的解析式；
（2）動直線y＝t與y軸交于點C，若CQ=3CP，求t的值；
（3）將拋物線y＝ax2＋bx－5在x軸下方的部分沿x軸翻折，若動直線y＝t與翻折后的圖像交于點M、N，點M、N能否是線段PQ的三等分點？若能，求PQ的長度；若不能，請說明理由．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
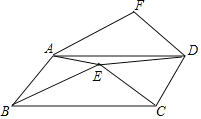
【題目】如圖，點E在ABCD的內部，AF∥BE，DF∥CE．
（1）求證
BCE≌ADF；
（2）若ABCD的面積為96cm2，求四邊形AEDF的面積．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
