
【題目】在Rt△ABC中,∠ACB=90°,BC=30,AB=50.點P是AB邊上任意一點,直線PE⊥AB,與邊AC或BC相交于E.點M在線段AP上,點N在線段BP上,EM=EN,sin∠EMP= ![]() .
.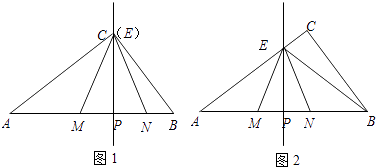
(1)如圖1,當點E與點C重合時,求CM的長;
(2)如圖2,當點E在邊AC上時,點E不與點A,C重合,設AP=x,BN=y,求y關于x的函數關系式,并寫出x的取值范圍;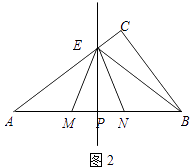
(3)若△AME∽△ENB,求AP的長.
【答案】
(1)
解:∵∠ACB=90°,
∴AC= ![]() =
= ![]() =40,
=40,
∵CP⊥AB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴CP=24,
∴CM= ![]() =
= ![]() =26
=26
(2)
解:∵sin∠EMP= ![]() ,
,
∴設EP=12a,
則EM=13a,PM=5a,
∵EM=EN,
∴EN=13a,PN=5a,
∵△AEP∽△ABC,
∴ ![]() ,
,
∴ ![]() =
= ![]()
∴x=16a,
∴a= ![]() ,
,
∴BP=50﹣16a,
∴y=50﹣21a,
=50﹣21× ![]() ,
,
=50﹣ ![]() x,
x,
∵當E點與A點重合時,x=0.當E點與C點重合時,x=32.
∴函數的定義域是:(0<x<32)
(3)
解:①當點E在AC上時,如圖2,
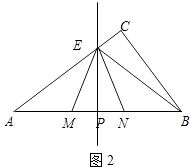
設EP=12a,則EM=13a,MP=NP=5a,
∵△AEP∽△ABC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AP=16a,
∴AM=11a,
∴BN=50﹣16a﹣5a=50﹣21a,
∵△AME∽△ENB,
∴ ![]() =
= ![]()
∴ ![]() =
= ![]() ,
,
∴a= ![]() ,
,
∴AP=16× ![]() =22,
=22,
②當點E在BC上時,如圖(備用圖),設EP=12a,則EM=13a,MP=NP=5a,
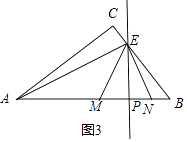
∵△EBP∽△ABC,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得BP=9a,
∴BN=9a﹣5a=4a,AM=50﹣9a﹣5a=50﹣14a,
∵△AME∽△ENB,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得a= ![]() ,
,
∴AP=50﹣9a=50﹣9× ![]() =42.
=42.
所以AP的長為:22或42.
【解析】((1)本題需先根據已知條件得出AC的值,再根據CP⊥AB求出CP,從而得出CM的值.(2)本題需先根據EN,根據sin∠EMP= ![]() ,設出EP的值,從而得出EM和PM的值,再得出△AEP∽△ABC,即可求出
,設出EP的值,從而得出EM和PM的值,再得出△AEP∽△ABC,即可求出 ![]() =
= ![]() ,求出a的值,即可得出y關于x的函數關系式,并且能求出函數的定義域.(3)本題需先設EP的值,得出則EM和MP的值,然后分①點E在AC上時,根據△AEP∽△ABC,求出AP的值,從而得出AM和BN的值,再根據△AME∽△ENB,求出a的值,得出AP的長;②點E在BC上時,根據△EBP∽△ABCC,求出AP的值,從而得出AM和BN的值,再根據△AME∽△ENB,求出a的值,得出AP的長.
,求出a的值,即可得出y關于x的函數關系式,并且能求出函數的定義域.(3)本題需先設EP的值,得出則EM和MP的值,然后分①點E在AC上時,根據△AEP∽△ABC,求出AP的值,從而得出AM和BN的值,再根據△AME∽△ENB,求出a的值,得出AP的長;②點E在BC上時,根據△EBP∽△ABCC,求出AP的值,從而得出AM和BN的值,再根據△AME∽△ENB,求出a的值,得出AP的長.
【考點精析】本題主要考查了相似三角形的應用的相關知識點,需要掌握測高:測量不能到達頂部的物體的高度,通常用“在同一時刻物高與影長成比例”的原理解決;測距:測量不能到達兩點間的舉例,常構造相似三角形求解才能正確解答此題.


 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ACB中,∠ACB=90°,∠A=30°,點D是AB邊的中點.
(1)如圖1,若CD=4,求△ACB的周長.
(2)如圖2,若E為AC的中點,將線段CE以C為旋轉中心順時針旋轉60°,使點E至點F處,連接BF交CD于點M,連接DF,取DF的中點N,連接MN,求證:MN=2CM.
(3)如圖3,以C為旋轉中心將線段CD順時針旋轉90°,使點D至點E處,連接BE交CD于M,連接DE,取DE的中點N,連接交MN,試猜想BD、MN、MC之間的關系,直接寫出其關系式,不證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知5臺A型機器一天的產品裝滿8箱后還剩4個,7臺B型機器一天的產品裝滿11箱后還剩1個,每臺A型機器比B型機器一天多生產1個產品.
(1)求每箱裝多少個產品.
(2)3臺A型機器和2臺B型機器一天能生產多少個產品?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現代互聯網技術的廣泛應用,催生了快遞行業的高速發展.小明計劃給朋友快遞一部分物品,經了解有甲、乙兩家快遞公司比較合適.甲公司表示:快遞物品不超過1千克的,按每千克22元收費;超過1千克,超過的部分按每千克15元收費.乙公司表示:按每千克16元收費,另加包裝費3元.設小明快遞物品x千克.
(1)請分別寫出甲、乙兩家快遞公司快遞該物品的費用y(元)與x(千克)之間的函數關系式;
(2)小明選擇哪家快遞公司更省錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數軸上,A、B兩點表示的數a,b滿足|a﹣6|+(b+12)2=0
(1)a= ,b= ;
(2)若小球M從A點向負半軸運動、小球N從B點向正半軸運動,兩球同時出發,小球M運動的速度為每秒2個單位,當M運動到OB的中點時,N點也同時運動到OA的中點,則小球N的速度是每秒 個單位;
(3)若小球M、N保持(2)中的速度,分別從A、B兩點同時出發,經過 秒后兩個小球相距兩個單位長度.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:E是邊長為1的正方形ABCD的對角線BD上一點,且BE=BC,P為CE上任意一點,PQ⊥BC于點Q,PR⊥BE于點R,則PQ+PR的值是( ) 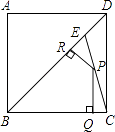
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為發展校園足球運動,某縣城區四校決定聯合購買一批足球運動裝備,市場調查發現:甲、乙兩商場以同樣的價格出售同種品牌的足球隊服和足球,已知每套隊服比每個足球多50元,兩套隊服與三個足球的費用相等.經洽談,甲商場的優惠方案是:每購買10套隊服,送1個足球;乙商場的優惠方案是:若購買隊服超過80套,則購買足球打八折.
(1)每套隊服和每個足球的價格分別是多少?
(2)若城區四校聯合購買100套隊服和a個足球,請用含a的式子分別表示出到甲商場和乙商場購買裝備所需的費用.
(3)假如你是本次購買任務的負責人,你認為到哪家商場購買比較合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市團委舉行以“我的中國夢”為主題的知識競賽,甲、乙兩所學校的參賽人數相等,比賽結束后,發現學生成績分別為![]() 分,
分,![]() 分,
分,![]() 分,
分,![]() 分,并根據統計數據繪制了如下不完整的統計圖表:
分,并根據統計數據繪制了如下不完整的統計圖表:
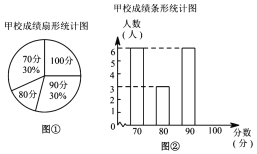
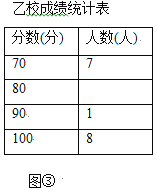
(1)乙學校的參賽人數是 人;
(2)在圖①中,“![]() 分”所在扇形的圓心角度數為 ;
分”所在扇形的圓心角度數為 ;
(3)請你將圖②補充完整;
(4)求乙校成績的平均分;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com