
【題目】問題探究
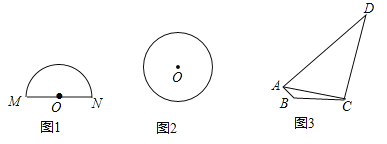
(1)如圖1,請在半徑為![]() 的半圓
的半圓![]() 內(nèi)(含弧和直徑
內(nèi)(含弧和直徑![]() )畫出面積最大的三角形,并求出這個三角形的面積;
)畫出面積最大的三角形,并求出這個三角形的面積;
(2)如圖2,請在半徑為![]() 的
的![]() 內(nèi)(含弧)畫出面積最大的矩形
內(nèi)(含弧)畫出面積最大的矩形![]() ,并求出這個矩形的面積;
,并求出這個矩形的面積;
問題解決
(3)如圖3,![]() 是一塊草坪,其中
是一塊草坪,其中![]() ,
,![]() ,
,![]() ,某開發(fā)商現(xiàn)準備再征一塊地,把
,某開發(fā)商現(xiàn)準備再征一塊地,把![]() 擴充為四邊形
擴充為四邊形![]() ,使
,使![]() ,是否存在面積最大的四邊形
,是否存在面積最大的四邊形![]() ?若存在,求出四邊形
?若存在,求出四邊形![]() 的最大面積;若不存在,請說明理由.(結(jié)果保留根號)
的最大面積;若不存在,請說明理由.(結(jié)果保留根號)
【答案】(1)圖形見解析;![]() ;(2)圖形見解析;
;(2)圖形見解析;![]() 矩形
矩形![]() ;(3)存在,最大面積為
;(3)存在,最大面積為![]() .
.
【解析】
(1)過圓心O作直徑的垂線得到最大的![]() ,求面積即可;
,求面積即可;
(2)作兩條互相垂直的直徑,作對角線,連成的四邊形即為最大的矩形,求其面積即可;
(3)如圖3,過A作AE⊥BC,交CB的延長線于E,分別求出EC、AE、AC的長,求![]() 的面積,在
的面積,在![]() 中,AC是定值,∠D=30°是定值,畫
中,AC是定值,∠D=30°是定值,畫![]() 的外接圓O,由圖3可知:當D點與AC的距離最大時,
的外接圓O,由圖3可知:當D點與AC的距離最大時,![]() 的面積最大,設(shè)AC的中垂線交⊙O于
的面積最大,設(shè)AC的中垂線交⊙O于![]() ,交AC于F,則
,交AC于F,則![]() 即為D點與AC的最大距離,求出
即為D點與AC的最大距離,求出![]() ,代入面積公式求面積即可.
,代入面積公式求面積即可.
解:(1)如圖1,過點![]() 作
作![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() 、
、![]() ,則
,則![]() 即為所求.
即為所求.
![]()
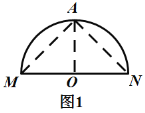
(2)如圖2,過點![]() 作
作![]() 的任一直徑
的任一直徑![]() ,再過點
,再過點![]() 作
作![]() ,交
,交![]() 于點
于點![]() 、
、![]() ,連接
,連接![]() 、
、![]() 、
、![]() 、
、![]() ,則矩形
,則矩形![]() 即為所求.
即為所求.
![]() 矩形
矩形![]() ;
;
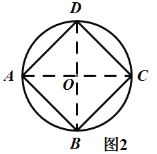
(3)存在面積最大的四邊形![]() ,理由如下:
,理由如下:
如圖3,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() .
.
![]() ,
,
![]() .
.
在![]() 中,
中,![]() 是定值,
是定值,![]() 是定值,
是定值,
如圖3,![]() 、
、![]() 、
、![]() 三點在同一
三點在同一![]() 上(作
上(作![]() 、
、![]() 的中垂線,交點即為圓心
的中垂線,交點即為圓心![]() ),
),
![]() 的長度一定,
的長度一定,
![]() 當
當![]() 點與
點與![]() 的距離最大時,
的距離最大時,![]() 的面積最大.
的面積最大.
設(shè)![]() 的中垂線交
的中垂線交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,
,
則![]() 即為
即為![]() 點與
點與![]() 的最大距離.
的最大距離.
![]() ,
,
連接![]() 、
、![]() ,則
,則![]() 。
。
![]() 是等邊三角形.
是等邊三角形.
![]() ,
,![]() .
.
∴![]() .
.
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]()
即四邊形![]() 的最大面積為
的最大面積為![]() .
.


 53隨堂測系列答案
53隨堂測系列答案科目:初中數(shù)學 來源: 題型:
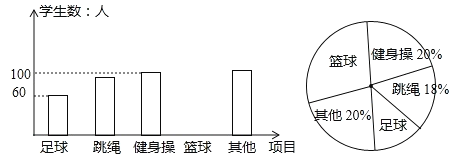
【題目】某市為提高學生參與體育活動的積極性,圍繞“你喜歡的體育運動項目(只寫一項)”這一問題,對初一新生進行隨機抽樣調(diào)查.下面是根據(jù)調(diào)查結(jié)果繪制成的統(tǒng)計圖(不完整).
請你根據(jù)圖中提供的信息解答下列問題:
(1)本次抽樣調(diào)查一共調(diào)查調(diào)查了多少名學生?
(2)根據(jù)條形統(tǒng)計圖中的數(shù)據(jù),求扇形統(tǒng)計圖中“最喜歡足球運動”的學生數(shù)對應(yīng)扇形的圓心角度數(shù).
(3)請將條形圖補充完整.
(4)若該市2017年約有初一新生21000人,請你估計全市本屆學生中“最喜歡足球運動”的學生有多少人?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】為響應(yīng)黨的“文化自信”號召,某校開展了古詩詞誦讀大賽活動,現(xiàn)隨機抽取部分同學的成績進行統(tǒng)計,并繪制成如下的兩個不完整的統(tǒng)計圖,請結(jié)合圖中提供的信息,解答下列問題:
(1)![]() _____,并把頻數(shù)分布直方圖補充完整;
_____,并把頻數(shù)分布直方圖補充完整;
(2)求扇形![]() 的圓心角度數(shù),成績眾數(shù)落在多少分之間;
的圓心角度數(shù),成績眾數(shù)落在多少分之間;
(3)如果全校有2000名學生參加這次活動,90分以上(含90分)為優(yōu)秀,那么估計獲得優(yōu)秀獎的學生有多少人?

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=3,BC=5,點P是BC邊上的一個動點(點P不與點B,C重合),現(xiàn)將△PCD沿直線PD折疊,使點C落下點C1處;作∠BPC1的平分線交AB于點E.設(shè)BP=x,BE=y,那么y關(guān)于x的函數(shù)圖象大致應(yīng)為( )
A.
B.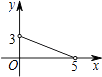
C.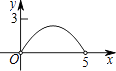
D.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,CN是等邊△ABC的外角∠ACM內(nèi)部的一條射線,點A關(guān)于CN的對稱點為D,連接AD,BD,CD,其中AD,BD分別交射線CN于點E,P.
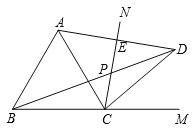
(1)求證:CD=CB;
(2)若∠ACN= a,求∠BDC的大小(用含a的式子表示);
(3)請判斷線段PB,PC與PE三者之間的數(shù)量關(guān)系,并證明你的結(jié)論.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
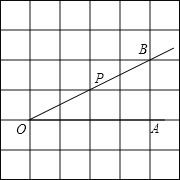
【題目】如圖,點P是∠AOB的邊OB上的一點.
(1)過點P畫OB的垂線,交OA于點C;
(2)過點P畫OA的垂線,垂足為H;
(3)線段PH的長度是點P到______的距離,______是點C到直線OB的距離,線段PC、PH、OC這三條線段大小關(guān)系是______(用“<”號連接).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
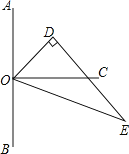
【題目】如圖,點O在直線AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先將△ODE一邊OE與OC重合,然后繞點O順時針方向旋轉(zhuǎn),當OE與OB重合時停止旋轉(zhuǎn).
(1)當OD在OA與OC之間,且∠COD=20°時,則∠AOE=______;
(2)試探索:在△ODE旋轉(zhuǎn)過程中,∠AOD與∠COE大小的差是否發(fā)生變化?若不變,請求出這個差值;若變化,請說明理由;
(3)在△ODE的旋轉(zhuǎn)過程中,若∠AOE=7∠COD,試求∠AOE的大小.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com