
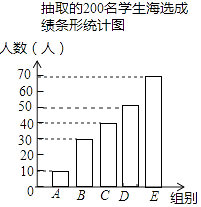
【題目】中華文明,源遠流長;中華詩詞,寓意深廣.為了傳承優秀傳統文化,我市某校團委組織了一次全校2000名學生參加的“中國詩詞大會”海選比賽,賽后發現所有參賽學生的成績均不低于50分,為了更好地了解本次海選比賽的成績分布情況,隨機抽取了其中200名學生的海選比賽成績(成績x取整數,總分100分)作為樣本進行整理,得到下列統計圖表: 抽取的200名學生海選成績分組表
組別 | 海選成績x |
A組 | 50≤x<60 |
B組 | 60≤x<70 |
C組 | 70≤x<80 |
D組 | 80≤x<90 |
E組 | 90≤x<100 |
請根據所給信息,解答下列問題: 
(1)請把圖1中的條形統計圖補充完整;(溫馨提示:請畫在答題卷相對應的圖上)
(2)在圖2的扇形統計圖中,記表示B組人數所占的百分比為a%,則a的值為 , 表示C組扇形的圓心角θ的度數為度;
(3)規定海選成績在90分以上(包括90分)記為“優等”,請估計該校參加這次海選比賽的2000名學生中成績“優等”的有多少人?
【答案】
(1)解:D的人數是:200﹣10﹣30﹣40﹣70=50(人),
補圖如下:
(2)15;72
(3)解:根據題意得:
2000× ![]() =700(人),
=700(人),
答:估計該校參加這次海選比賽的2000名學生中成績“優等”的有700人
【解析】(2)B組人數所占的百分比是 ![]() ×100%=15%, 則a的值是15;
×100%=15%, 則a的值是15;
C組扇形的圓心角θ的度數為360× ![]() =72°;
=72°;
故答案為:15,72;
(1)用隨機抽取的總人數減去A、B、C、E組的人數,求出D組的人數,從而補全統計圖;(2)用B組抽查的人數除以總人數,即可求出a;用360乘以C組所占的百分比,求出C組扇形的圓心角θ的度數;(3)用該校參加這次海選比賽的總人數乘以成績在90分以上(包括90分)所占的百分比,即可得出答案.


科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD頂點A、B在x軸上,點D在y軸上,函數y= ![]() (x>0)的圖象經過點C(2,3),直線AD交雙曲線于點E,并且EB⊥x軸,CD⊥y軸,EB與CD交于點F.
(x>0)的圖象經過點C(2,3),直線AD交雙曲線于點E,并且EB⊥x軸,CD⊥y軸,EB與CD交于點F.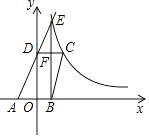
(1)若EB= ![]() OD,求點E的坐標;
OD,求點E的坐標;
(2)若四邊形ABCD為平行四邊形,求過A、D兩點的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線![]() 與雙曲線
與雙曲線![]() 交于
交于![]() 兩點,且點
兩點,且點![]() 的橫坐標為
的橫坐標為![]() .
.

(1)求![]() 的值;
的值;
(2)若雙曲線![]() 上一點
上一點![]() 的縱坐標為8,求
的縱坐標為8,求![]() 的面積;
的面積;
(3)過原點![]() 的另一條直線
的另一條直線![]() 交雙曲線
交雙曲線![]() 于
于![]() 兩點(
兩點(![]() 點在第一象限),若由點
點在第一象限),若由點![]() 為頂點組成的四邊形面積為
為頂點組成的四邊形面積為![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB=DB,∠1=∠2,請問添加下面哪個條件不能判斷△ABC≌△DBE的是( )

A. BC=BE B. ∠A=∠D C. ∠ACB=∠DEB D. AC=DE
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣(x﹣1)2+c與x軸交于A,B(A,B分別在y軸的左右兩側)兩點,與y軸的正半軸交于點C,頂點為D,已知A(﹣1,0).
(1)求點B,C的坐標;
(2)判斷△CDB的形狀并說明理由;
(3)將△COB沿x軸向右平移t個單位長度(0<t<3)得到△QPE.△QPE與△CDB重疊部分(如圖中陰影部分)面積為S,求S與t的函數關系式,并寫出自變量t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,點C在以AB為直徑的半圓上,∠CAB的平分線AD交BC于點D,⊙O經過A、D兩點,且圓心O在AB上.
(1)求證:BD是⊙O的切線.
(2)若 ![]() ,
, ![]() ,求⊙O的面積.
,求⊙O的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠A=90°,O是BC邊上一點,以O為圓心的半圓與AB邊相切于點D,與AC、BC邊分別交于點E、F、G,連接OD,已知BD=2,AE=3,tan∠BOD= ![]() .
. 
(1)求⊙O的半徑OD;
(2)求證:AE是⊙O的切線;
(3)求圖中兩部分陰影面積的和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com