
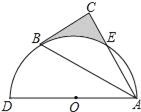
【題目】如圖,以AD為直徑的半圓O經過Rt△ABC斜邊AB的兩個端點,交直角邊AC于點E,B、E是半圓弧的三等分點,弧BE的長為![]() π,則圖中陰影部分的面積為( )
π,則圖中陰影部分的面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 考前必練系列答案
考前必練系列答案科目:初中數學 來源: 題型:
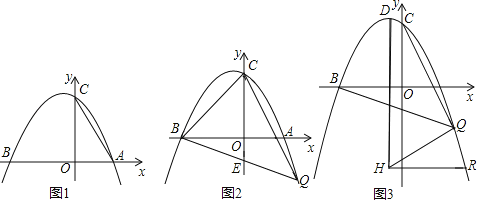
【題目】如圖,拋物線y=ax2+bx+5經過坐標軸上A、B和C三點,連接AC,tanC=![]() ,5OA=3OB.
,5OA=3OB.
(1)求拋物線的解析式;
(2)點Q在第四象限的拋物線上且橫坐標為t,連接BQ交y軸于點E,連接CQ、CB,△BCQ的面積為S,求S與t的函數解析式;
(3)已知點D是拋物線的頂點,連接CQ,DH所在直線是拋物線的對稱軸,連接QH,若∠BQC=45°,HR∥x軸交拋物線于點R,HQ=HR,求點R的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
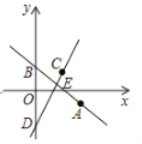
【題目】如圖,在平面直角坐標系中,直線![]() 過點
過點![]() 且與
且與![]() 軸交于點
軸交于點![]() .把點
.把點![]() 向左平移2個單位,再向上平移4個單位,得到點
向左平移2個單位,再向上平移4個單位,得到點![]() .過點
.過點![]() 的直線
的直線![]() 交
交![]() 軸于點
軸于點![]() .
.
(1)求直線![]() 的解析式.
的解析式.
(2)直線![]() 與
與![]() 交于點
交于點![]() ,在直線
,在直線![]() 和直線
和直線![]() 上是否存在點
上是否存在點![]() ,使
,使![]() ,若存在,求出點
,若存在,求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
(3)若有過點![]() 的直線
的直線![]() 與線段
與線段![]() 有公共點且滿足
有公共點且滿足![]() 隨
隨![]() 的增大而減小,設直線
的增大而減小,設直線![]() 與
與![]() 軸交點橫坐標為
軸交點橫坐標為![]() ,直接寫出
,直接寫出![]() 的取值范圍________.
的取值范圍________.
查看答案和解析>>
科目:初中數學 來源: 題型:
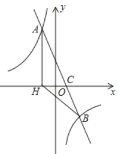
【題目】如圖,在平面直角坐標系中,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于
的圖象交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,點
,點![]() 是線段
是線段![]() 的中點,
的中點,![]() ,
,![]() ,點
,點![]() 的坐標為
的坐標為![]() .
.
(1)求該反比例函數和一次函數的解析式;
(2)求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=40°,連接BD、CE.將△ADE繞點A旋轉,BD、CE也隨之運動.
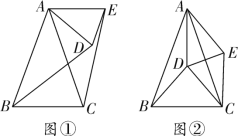
(1)求證:BD=CE;
(2)在△ADE繞點A旋轉過程中,當AE∥BC時,求∠DAC的度數;
(3)如圖②,當點D恰好是△ABC的外心時,連接DC,判斷四邊形ADCE的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABDE是平行四邊形,C為邊B D延長線上一點,連結AC、CE,使AB=AC.
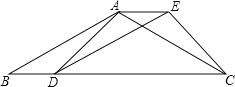
(1)求證:△BAD≌△AEC;
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四邊形ABDE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
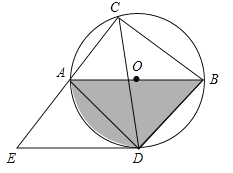
【題目】如圖,⊙O的直徑AB=10,弦AC=6,∠ACB的平分線交⊙O于D,過點D作DE∥AB交CA的延長線于點E,連接AD,BD.
(1)由AB,BD,![]() 圍成的曲邊三角形的面積是 ;
圍成的曲邊三角形的面積是 ;
(2)求證:DE是⊙O的切線;
(3)求線段DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地區一種商品的需求量y1(單位:萬件)、供應量y2(單位;萬件)與價格x(單位:元/件)分別近似滿足下列函數關系式:y1=-x+60,y2=2x-36.需求量為0時,即停止供應.當y1=y2時,該商品的價格稱為穩定價格,需求量稱為穩定需求量.
(1)求該商品的穩定價格與穩定需求量;
(2)價格在什么范圍時,該商品的需求量低于供應量;
(3)當需求量高于供應量時,政府常通過對供應方提供價格補貼來提高供貨價格,以提高供應量.現若要使穩定需求量增加4萬件,政府應對每件商品提供多少元補貼才能使供應量等于需求量?
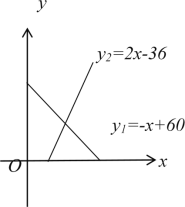
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系,點 O 是原點,直線 y x 6分別交 x 軸,y 軸于點 B,A,經過點 A 的直線 y x b 交 x 軸于點 C.
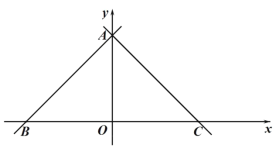
(1)求 b 的值 ;
(2)點 D 是線段 AB 上的一個動點,連接 OD,過點 O 作 OE⊥OD 交 AC 于點 E,連接DE,將△ODE 沿 DE 折疊得到△FDE,連接 AF.設點 D 的橫坐標為 t,AF 的長為 d,當t> 3 時,求 d 與 t 之間的函數關系式(不要求寫出自變量 t 的取值范圍);
(3)在(2)的條件下,DE 交 OA 于點 G,且 tan∠AGD=3.點 H 在 x 軸上(點 H 在點O 的右側),連接 DH,EH,FH,當∠DHF=∠EHF 時,請直接寫出點 H 的坐標,不需要寫出解題過程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com