【題目】如圖，
，求證：
，請將證明過程填寫完整.
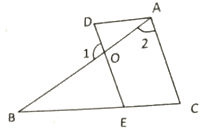
證明：∵
（已知）
又∵
（ ）
∴________
，
∴
____________（ ）
∴
______________（ ）
又∵
（已知）
∴
________________，
∴（ ）
科目：初中數學 來源： 題型：
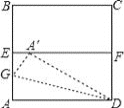
【題目】如圖，ABCD是一張邊長為4cm的正方形紙片，E，F分別為AB，CD的中點，沿過點D的折痕將A 角翻折，使得點A落在EF上的點A′處，折痕交AE于點G，則EG=_________cm．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在以
為原點的平面直角坐標系中，有不在坐標軸上的兩個點
、
，設的坐標為
，點的坐標
（1）若
與坐標軸平行，則
；
（2）若
、
、
滿足
和
，
軸，垂足為
，
軸，垂足為
.
①求四邊形
的面積；
②連、
、
，若
的面積大于
而不大于
，求的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC中，∠BAC=100°，∠ABC=∠ACB，點D在直線BC上運動（不與點B、C重合），點E在射線AC上運動，且∠ADE=∠AED，設∠DAC=n．
（1）如圖（1），當點D在邊BC上時，且n=36°，則∠BAD= _________，∠CDE= _________.
（2）如圖（2），當點D運動到點B的左側時，其他條件不變，請猜想∠BAD和∠CDE的數量關系，并說明理由.
（3）當點D運動到點C的右側時，其他條件不變，∠BAD和∠CDE還滿足（2）中的數量關系嗎？請畫出圖形，并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，四邊形ABCD四條邊上的中點分別為E、F、G、H，順次連接EF、FG、GH、HE，得到四邊形EFGH（即四邊形ABCD的中點四邊形）.
（1）四邊形EFGH的形狀是 _____________ ，（證明你的結論. ）
（2）當四邊形ABCD的對角線滿足 __________條件時，四邊形EFGH是矩形(不用證明)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中有三個點
，
是
的邊
上一點，經平移后得到
，點
的對應點為
.
（1）畫出平移后的，寫出點
的坐標；
（2）的面積為_________________；
（3）若點
是
軸上一動點，
的面積為
，求與
之間的關系式（用含的式子表示）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，在等邊三角形ABC中，BC＝8cm，射線AG∥BC，點E從點A出發沿射線AG以1cm/s的速度運動，同時點F從點B出發沿射線BC以2cm/s的速度運動，設運動時間為t（s）．
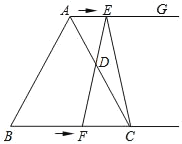
（1）連接EF，當EF經過AC邊的中點D時，求證：四邊形AFCE是平行四邊形；
（2）填空：①當t為 s時，四邊形ACFE是菱形；②當t為 s時，△ACE的面積是△ACF的面積的2倍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形
的頂點
、
分別在
、
軸的正半軸上，點
在反比例函數
的第一象限內的圖像上，
，
，動點
在軸的上方，且滿足
.
（1）若點在這個反比例函數的圖像上，求點的坐標；
（2）連接
、
，求
的最小值；
（3）若點
是平面內一點，使得以、、、為頂點的四邊形是菱形，則請你直接寫出滿足條件的所有點的坐標.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一只貓頭鷹蹲在一棵樹AC的B（點B在AC上）處，發現一只老鼠躲進短墻DF的另一側，貓頭鷹的視線被短墻遮住，為了尋找這只老鼠，它又飛至樹頂C處，已知短墻高DF＝4米，短墻底部D與樹的底部A的距離為2.7米，貓頭鷹從C點觀測F點的俯角為53°，老鼠躲藏處M（點M在DE上）距D點3米．（參考數據：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
（1）貓頭鷹飛至C處后，能否看到這只老鼠？為什么？
（2）要捕捉到這只老鼠，貓頭鷹至少要飛多少米（精確到0.1米）？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
