
【題目】在△ABC 中,AB=AC,點 M 在 BA 的延長線上,點 N 在 BC 的延長線上,過點 C 作CD∥AB 交∠CAM 的平分線于點 D.
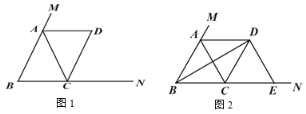
(1)如圖 1,求證:四邊形 ABCD 是平行四邊形;
(2)如圖 2,當∠ABC=60°時,連接 BD,過點 D 作 DE⊥BD,交 BN 于點 E,在不添加任何輔助線的情況下,請直接寫出圖 2 中四個三角形(不包含△CDE),使寫出的每個三角形的面積與△CDE 的面積相等.
【答案】(1)見解析;(2)△ABC、△DBC、△ABD、△ACD.
【解析】
(1)根據等腰三角形的性質和三角形外角的性質可得∠CAM=2∠ABC,根據角平分線的定義可得∠CAM=2∠MAD,等量代換得到∠ABC=∠MAD,進而證得AD∥BC即可解決問題;
(2)首先證明平行四邊形ABCD是菱形,然后證明△DCE是等邊三角形,得到CE=CD=BC=AD,根據等底等高的三角形面積相等可得答案.
解:(1)∵AB=AC,
∴∠ABC=∠ACB,
∴∠CAM=∠ABC+∠ACB=2∠ABC,
∵AD是∠CAM 的平分線,
∴∠CAM=2∠MAD,
∴∠ABC=∠MAD,
∴AD∥BC,
∵CD∥AB,
∴四邊形ABCD是平行四邊形;
(2)∵∠ABC=60°,AB=AC,四邊形ABCD是平行四邊形,
∴△ABC是等邊三角形,∠DCE=∠ABC=60°,
∴AB=BC,
∴平行四邊形ABCD是菱形,
∴∠DBE=30°,
∵DE⊥BD,
∴∠DEB=60°,
∴△DCE是等邊三角形,
∴CE=CD=BC=AD,
∵AD∥BC,
∴△ABC、△DBC、△ABD、△ACD的面積都與△CDE的面積相等.


科目:初中數學 來源: 題型:
【題目】2018年9月17日世界人工智能大會在.上海召開,人工智能的變革力在教育、制造等領域加速落地.在某市舉辦的一次中學生機器人足球賽中,有四個代表隊進入決賽,決賽中,每個隊分別與其它三個隊進行主客場比賽各一場(即每個隊要進行6場比賽),以下是積分表的一-部分.
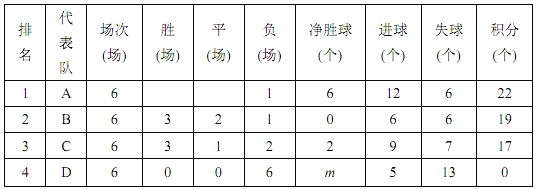
(說明:積分=勝場積分十平場積分+負場積分)
(1)D代表隊的凈勝球數m=______;
(2)本次決賽中,勝一場積______分,平一場積______分,負一場積_______分;
(3)此次競賽的獎金分配方案為:進入決賽的每支代表隊都可以獲得參賽獎金6000元;另外,在決賽期間,每勝一場可以再獲得獎金2000元,每平一場再獲得獎金1000元.請根據表格提供的信息,求出冠軍A隊一共能獲得多少獎金.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題提出
(1)如圖①,在矩形ABCD中,AB=2AD,E為CD的中點,則∠AEB ∠ACB(填“>”“<”“=”);
問題探究
(2)如圖②,在正方形ABCD中,P為CD邊上的一個動點,當點P位于何處時,∠APB最大?并說明理由;
問題解決
(3)如圖③,在一幢大樓AD上裝有一塊矩形廣告牌,其側面上、下邊沿相距6米(即AB=6米),下邊沿到地面的距離BD=11.6米.如果小剛的睛睛距離地面的高度EF為1.6米,他從遠處正對廣告牌走近時,在P處看廣告效果最好(視角最大),請你在圖③中找到點P的位置,并計算此時小剛與大樓AD之間的距離.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某家具生產廠生產某種配套桌椅(一張桌子,兩把椅子),已知每塊板材可制作桌子![]() 張或椅子
張或椅子![]() 把,現計劃用
把,現計劃用![]() 塊這種板材生產一批桌椅(不考慮板材的損耗,恰好配套),設用
塊這種板材生產一批桌椅(不考慮板材的損耗,恰好配套),設用![]() 塊板材做椅子,用
塊板材做椅子,用![]() 塊板材做桌子,則下列方程組正確的是( )
塊板材做桌子,則下列方程組正確的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市擬于中秋節前![]() 天里銷售某品牌月餅,其進價為
天里銷售某品牌月餅,其進價為![]() 元/
元/![]() .設第
.設第![]() 天的銷售價格為
天的銷售價格為![]() (元/
(元/![]() )銷售量為
)銷售量為![]() .該超市根據以往的銷售經驗得出以下的銷售規律:①與
.該超市根據以往的銷售經驗得出以下的銷售規律:①與![]() 滿足一次函數關系,且當
滿足一次函數關系,且當![]() 時,
時,![]() ;
;![]() 時,
時,![]() .②
.②![]() 與
與![]() 的關系為
的關系為![]() .
.
(1)![]() 與
與![]() 的關系式為________;
的關系式為________;
(2)當![]() 時,求第幾天的銷售利潤
時,求第幾天的銷售利潤![]() (元)最大?最大利潤為多少?
(元)最大?最大利潤為多少?
(3)若在當天銷售價格的基礎上漲![]() 元/
元/![]() ,在第
,在第![]() 天至
天至![]() 天銷售利潤最大值為
天銷售利潤最大值為![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校計劃為疫情期間表現優秀的學生購買獎品.已知購買![]() 個
個![]() 獎品和
獎品和![]() 個
個![]() 獎品共需
獎品共需![]() 元;購買
元;購買![]() 個
個![]() 獎品和
獎品和![]() 個
個![]() 獎品共需
獎品共需![]() 元
元
(1)求![]() 兩種獎品的單價;
兩種獎品的單價;
(2)學校準備購買![]() 兩種獎品共
兩種獎品共![]() 個,且
個,且![]() 獎品的數量不少于
獎品的數量不少于![]() 獎品數量的一半,請設計出最省錢的購買方案,并說明理由.
獎品數量的一半,請設計出最省錢的購買方案,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】五一小長假前夕,某服裝店的老板到服裝廠購買男士夏裝和女士夏裝.已知購進![]() 套男士夏裝和
套男士夏裝和![]() 套女士夏裝需要
套女士夏裝需要![]() 元;購進
元;購進![]() 套男士夏裝和
套男士夏裝和![]() 套女士夏裝需要
套女士夏裝需要![]() 元.
元.
(1)求男士夏裝和女士夏裝每套進價分別是多少元;
(2)若![]() 套男士夏裝的售價為
套男士夏裝的售價為![]() 元,
元,![]() 套女士夏裝的售價為
套女士夏裝的售價為![]() 元,時裝店決定購進男士夏裝的數量為女士夏裝的數量的
元,時裝店決定購進男士夏裝的數量為女士夏裝的數量的![]() 還多
還多![]() 套,如果購進的男士夏裝和女士夏裝全部售出后的總利潤超過
套,如果購進的男士夏裝和女士夏裝全部售出后的總利潤超過![]() 元,那么此次至少可購進多少套女士夏裝?
元,那么此次至少可購進多少套女士夏裝?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】詩詞是中華民族燦爛文化中的瑰寶,王老師連續三個月在班上開展針對全班同學的古詩詞默寫的測試活動.如圖,王老師將三次默寫的成績(滿分10分)做了統計,并繪制了折線統計圖.由圖可知,以下結論錯誤的是( )
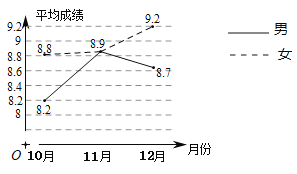
A.男、女生11月份的平均成績相同
B.10月到12月,女生的平均成績一直在進步
C.10月到11月,女生的平均成績的增長率約為8.5%
D.11月到12月女生的平均成績比10月到11月的增長快
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com