
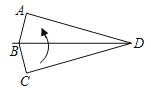
【題目】定義:有一組對角互補的四邊形叫做互補四邊形,如圖,在互補四邊形紙片ABCD中,BA=BC,AD=CD,∠A=∠C=90°,∠ADC=30°.將紙片先沿直線BD對折,再將對折后的紙片從一個頂點出發的直線裁剪,把剪開的紙片打開后鋪平,若鋪平后的紙片中有一個面積為4的平行四邊形,則CD的長為__.
【答案】2![]() +4
+4![]() 或
或![]() +2
+2![]() .
.
【解析】
根據題意結合裁剪的方法得出符合題意的圖形有兩個,分別利用菱形的判定與性質以及勾股定理得出CD的長.
解:如圖1所示:從頂點A(或C)剪開紙片,四邊形ABCE是平行四邊形,
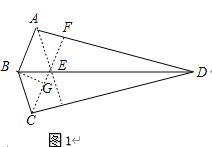
根據題意可知:
∵BA=BC,AD=CD,∠A=∠C=90°
∴△ABD≌△CBD(SAS)
∴∠ABD=∠CBD=75°,
∵四邊形ABCE是面積為4的平行四邊形,AB=CB
∴ABCE是菱形,
∴△BCE的面積為2,CB=CE=AB,
∴∠BCE=30°,
作BG⊥CE于點G,
∴BC=2BG,
∴CE=2BG,
∴S△BCE=![]() CEBG=2
CEBG=2
∴BG2=2,
∴BG=![]() ,CE=2
,CE=2![]() ,
,
∴CG=![]() BG=
BG=![]() ,
,
∴CF=CG+GF=CG+AB=CG+CE=![]() +2
+2![]() .
.
∵∠ADC=30°,∠CFD=90°
∴CD=2CF=2![]() +4
+4![]() .
.
如圖2,從頂點B剪開紙片,當四邊形BEDF是平行四邊形時,
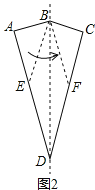
∵BE=BF,
∴平行四邊形BEDF是菱形,
∵∠A=∠C=90°,∠B=150°,
∴∠ADB=∠BDC=15°,
∵BE=DE,
∴∠AEB=30°,
∴設AB=y,則BE=2y,AE= ![]() y,
y,
∴DE=2y,
∵四邊形BEDF面積為4,
∴AB×DE=4,
即2y2=4,
解得:y=![]() ,
,
故AE=![]() ,DE=2
,DE=2![]() ,
,
則CD=AD=![]() +2
+2![]() ,
,
綜上所述:CD的值為:2![]() +4
+4![]() 或
或![]() +2
+2![]() .
.
故答案為2![]() +4
+4![]() 或
或![]() +2
+2![]() .
.


 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作業本系列答案
名校作業本系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知正比例函數y=2x和反比例函數的圖象交于點A(m,﹣2).

(1)求反比例函數的解析式;
(2)觀察圖象,直接寫出正比例函數值大于反比例函數值時自變量x的取值范圍;
(3)若雙曲線上點C(2,n)沿OA方向平移![]() 個單位長度得到點B,判斷四邊形OABC的形狀并證明你的結論.
個單位長度得到點B,判斷四邊形OABC的形狀并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,拋物線
,拋物線![]() 經過點
經過點![]() 、
、![]() .
.
(1)求![]() 、
、![]() 滿足的關系式及
滿足的關系式及![]() 的值.
的值.
(2)當![]() 時,若
時,若![]() 的函數值隨
的函數值隨![]() 的增大而增大,求
的增大而增大,求![]() 的取值范圍.
的取值范圍.
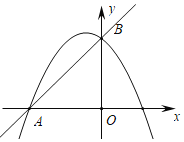
(3)如圖,當![]() 時,在拋物線上是否存在點
時,在拋物線上是否存在點![]() ,使
,使![]() 的面積為1?若存在,請求出符合條件的所有點
的面積為1?若存在,請求出符合條件的所有點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
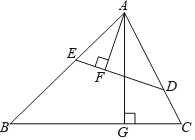
【題目】如圖在銳角三角形ABC中,點D,E分別在邊AC,AB上,AG⊥BC于點G,AF⊥DE于點F,∠EAF=∠GAC.
(1)求證:△ADE∽△ABC;
(2)如AF=3,AG=5,求△ADE與△ABC的周長之比.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于反比例函![]() ,下列說法中不正確的是( )
,下列說法中不正確的是( )
A.點![]() 在它的圖象上
在它的圖象上
B.它的圖象在第一、三象限
C.當![]() 時,
時,![]() 隨
隨![]() 的增大而減小
的增大而減小
D.如果點![]() 在它的圖象上,則點
在它的圖象上,則點![]() 不在它的圖象上
不在它的圖象上
查看答案和解析>>
科目:初中數學 來源: 題型:
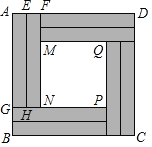
【題目】某公司對自家辦公大樓一塊![]() 米的正方形墻面進行了如圖所示的設計裝修(四周陰影部分是八個全等的矩形,用材料甲裝修;中心區是正方形
米的正方形墻面進行了如圖所示的設計裝修(四周陰影部分是八個全等的矩形,用材料甲裝修;中心區是正方形![]() ,用材料乙裝修). 兩種材料的成本如下表:
,用材料乙裝修). 兩種材料的成本如下表:
材料 | 甲 | 乙 |
價格(元/米2) | 550 | 500 |
設矩形的較短邊![]() 的長為
的長為![]() 米,裝修材料的總費用為
米,裝修材料的總費用為![]() 元.
元.
(1)計算中心區的邊![]() 的長(用含
的長(用含![]() 的代數式表示);
的代數式表示);
(2)求![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(3)當中心區的邊長![]() 不小于2米時,預備材料的購買資金32000元夠用嗎?請利用函數的增減性來說明理由.
不小于2米時,預備材料的購買資金32000元夠用嗎?請利用函數的增減性來說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
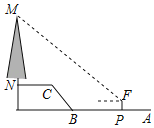
【題目】如圖,MN是垂直于水平面的一棵樹,小馬(身高1.70米)從點A出發,先沿水平方向向左走2米到達P點處,在P處測得大樹的頂端M的仰角為37°,再沿水平方向向左走8米到B點,再經過一段坡度i=4:3,坡長為5米的斜坡BC到達C點,然后再沿水平方向向左行走5米到達N點(A、B、C、N在同一平面內),則大樹MN的高度約為( )(參考數據:tan37°≈0.75,sin37°≈0.60)
A.7.8米B.9.7米C.12米D.13.7米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店經銷甲、乙兩種商品,已知一件甲種商品和一件乙種商品的進價之和為30元,每件甲種商品的利潤是4元,每件乙種商品的售價比其進價的2倍少11元,小明在該商店購買8件甲種商品和6件乙種商品一共用了262元.
(1)求甲、乙兩種商品的進價分別是多少元;
(2)在(1)的前提下,經銷商統計發現,平均每天可售出甲種商品400件和乙種商品300件,如果將甲種商品的售價每提高0.1元,則每天將少售出7件甲種商品;如果將乙種商品的售價每提高0.1元,則每天將少售出8件乙種商品,經銷商決定把兩商品的價格都提高a元,在不考慮其他因素的條件下,當a為多少時,才能使該經銷商每天銷售甲、乙兩種商品獲取的利潤共2500元.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com