
【題目】某數學老師為了了解學生在數學學習中常見錯誤的糾正情況,收集整理了學生在作業和考試中的常見錯誤,編制了10道選擇題,每題3分,對他所教的初三(1)班、(2)班進行了檢測,如圖表示從兩班各隨機抽取的10名學生的得分情況.
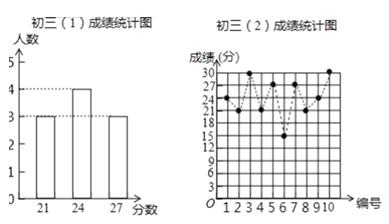
(1)利用圖中提供的信息,補全下表:
班級 | 平均數/分 | 中位數/分 | 眾數/分 | 方差/分 |
初三(1)班 | 24 | 24 | ________ | 5.4 |
初三(2)班 | 24 | _________ | 21 | ________ |
(2)哪個班的學生糾錯的得分更穩定?若把24分以上(含24分)記為“優秀”,兩班各40名學生,請估計兩班各有多少名學生成績優秀;
(3)現從兩個班抽取了數學成績最好的甲、乙、丙、丁四位同學,并隨機分成兩組進行數學競賽,求恰好選中甲、乙一組的概率.
【答案】(1)24,24,![]() ;(2)初三(1)班糾錯的得分更穩定;兩班各有28、24人成績優秀;(3)
;(2)初三(1)班糾錯的得分更穩定;兩班各有28、24人成績優秀;(3)![]() .
.
【解析】
(1)根據方差、中位數和眾數的定義進行解答即可;
(2)根據方差判斷穩定性,找到樣本中24分和24分以上人數所占的比值,用樣本平均數估計總體平均數;
(3)通過畫樹狀圖或列表即可求出概率.
解:(1)初三(1)班有4名學生24分,最多,故眾數為24,
把初三(2)班的成績從小到大排列,則處于中間位置的數為24和24,故中位數為24分,
初三(2)班成績的方差為
![]() ;
;
將數據填入表中為
班級 | 平均數/分 | 中位數/分 | 眾數/分 | 方差/分 |
初三(1)班 | 24 | 24 | 24 | 5.4 |
初三(2)班 | 24 | 24 | 21 | 19.8 |
(2)∵5.4<19.8,初三(1)班成績的方差小,
∴初三(1)班糾錯的得分更穩定;
初三(1)班成績優秀人數為![]() (人),
(人),
初三(2)班成績優秀人數為![]() (人);
(人);
(3)根據題意畫樹狀圖如下: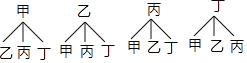
∵共有12種等可能的結果,甲、乙分在同一組的有2種情況,
∴甲、乙分在同一組的概率為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC,∠ACB=90°,BC=3,AC=4,小紅按如下步驟作圖:
①分別以A、C為圓心,以大于![]() AC的長為半徑在AC兩邊作弧,交于兩點M、N;
AC的長為半徑在AC兩邊作弧,交于兩點M、N;
②連接MN,分別交AB、AC于點D、O;
③過C作CE∥AB交MN于點E,連接AE、CD.
則四邊形ADCE的周長為( )

A. 10 B. 20 C. 12 D. 24
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下表是小安填寫的數學實踐活動報告的部分內容
題 目 | 測量鐵塔頂端到地面的高度 | |
測量目標示意圖 |
|
|
相關數據 | CD=20m,ɑ=45°,β=52° | |
求鐵塔的高度FE(結果精確到1米)(參考數據:sin52°≈0.79, cos52°≈0.62,tan52°≈1.28)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙兩個工廠同時加工一批機器零件.甲工廠先加工了兩天后停止加工,維修設備,當維修完設備時,甲乙兩廠加工的零件數相等,甲工廠再以原來的工作效率繼續加工這批零件.甲乙兩廠加工零件的數量![]() (件),
(件),![]() (件)與加工件的時間
(件)與加工件的時間![]() (天)的函數圖象如圖所示,
(天)的函數圖象如圖所示,

(1)乙工廠每天加工零件的數為_____件;
(2)甲工廠維修設備的時間是多少天?
(3)求甲維修設備后加工零件的數量![]() (件)與加工零件的時間
(件)與加工零件的時間![]() (天)的函數關系式,并寫出自變量
(天)的函數關系式,并寫出自變量![]() 的取值范圍
的取值范圍
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,與直線
兩點,與直線![]() 交于
交于![]() 、
、![]() 兩點,直線
兩點,直線![]() 與
與![]() 軸交于點
軸交于點![]() .
.
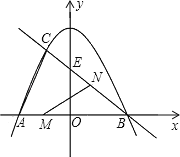
(1)求直線![]() 的解析式:
的解析式:
(2)若點![]() 在線段
在線段![]() 上以每秒1個單位長度的速度從點
上以每秒1個單位長度的速度從點![]() 向點
向點![]() 運動(不與點
運動(不與點![]() 、
、![]() 重合),同時,點
重合),同時,點![]() 在射線
在射線![]() 上以每秒2個單位長度的速度從點
上以每秒2個單位長度的速度從點![]() 向點
向點![]() 方向運動,設運動的時間為
方向運動,設運動的時間為![]() 秒,
秒,![]() 的面積為
的面積為![]() ,求
,求![]() 關于
關于![]() 的函數關系式,并求
的函數關系式,并求![]() 取何值時,
取何值時,![]() 最大?最大值是多少?
最大?最大值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著新冠肺炎的爆發,市場對口罩的需求量急劇增大.某口罩生產商自二月份以來,--直積極恢復產能,每日口罩生產量![]() (百萬個)與天數
(百萬個)與天數![]() 且
且![]() 為整數)的函數關系圖象如圖所示,而該生產商對口供應市場對口罩的需求量<(百萬個)與天數
為整數)的函數關系圖象如圖所示,而該生產商對口供應市場對口罩的需求量<(百萬個)與天數![]() 呈拋物線型,第
呈拋物線型,第![]() 天市場口罩缺口(需求量與供應量差)就達到
天市場口罩缺口(需求量與供應量差)就達到![]() (百萬個),之后若干天,市場口罩需求量不斷上升,在第
(百萬個),之后若干天,市場口罩需求量不斷上升,在第![]() 天需求量達到最高峰
天需求量達到最高峰![]() (百萬個).
(百萬個).
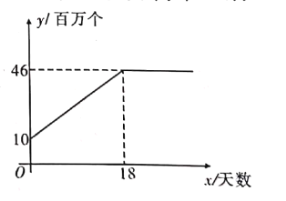
![]() 求出
求出![]() 與
與![]() 的函數解析式;
的函數解析式;
![]() 當市場供應量不小于需求量時,市民買口罩才無需提前預約,那么在整個二月份,市民無需預約即可購買口罩的天數共有多少天?
當市場供應量不小于需求量時,市民買口罩才無需提前預約,那么在整個二月份,市民無需預約即可購買口罩的天數共有多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖點A,E,F,C在同一直線上,AE=EF=FC,過E,F分別作DE⊥AC,BF⊥AC,連結AB,CD,BD,BD交AC于點G,若AB=CD.
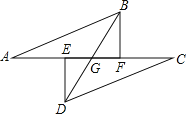
(1)求證:△ABF≌△CDE.
(2)若AE=ED=2,求BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】矩形紙片ABCD中,已知AD=8,AB=6,E是邊BC上的點,以AE為折痕折疊紙片,使點B落在點F處,連接FC,當△EFC為直角三角形時,BE的長為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在歌唱比賽中,一位歌手分別轉動如下的兩個轉盤(每個轉盤都被分成3等份)一次,根據指針指向的歌曲名演唱兩首曲目.

(1)轉動轉盤①時,該轉盤指針指向歌曲“3”的概率是 ;
(2)若允許該歌手替換他最不擅長的歌曲“3”,即指針指向歌曲“3”時,該歌手就選擇自己最擅長的歌曲“1”, 請用樹形圖或列表法中的一種,求他演唱歌曲“1”和“4”的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com