
【題目】2015年是中國人民抗日戰爭暨世界反法西斯戰爭勝利70周年,9月3日全國各地將舉行有關紀念活動.為了解初中學生對二戰歷史的知曉情況,某初中課外興趣小組在本校學生中開展了專題調查活動,隨機抽取了部分學生進行問卷調查,根據學生的答題情況,將結果分為![]() 、
、![]() 、
、![]() 、
、![]() 四類,其中
四類,其中![]() 類表示“非常了解”,
類表示“非常了解”,![]() 類表示“比較了解”,
類表示“比較了解”,![]() 類表示“基本了解”;
類表示“基本了解”;![]() 類表示“不太了解”,調查的數據經整理后形成尚未完成的條形統計圖(如圖①)和扇形統計圖(如圖②):
類表示“不太了解”,調查的數據經整理后形成尚未完成的條形統計圖(如圖①)和扇形統計圖(如圖②):
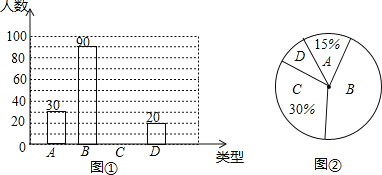
(1)在這次抽樣調查中,一共抽查了 名學生;
(2)請把圖①中的條形統計圖補充完整;
(3)圖②的扇形統計圖中![]() 類部分所對應扇形的圓心角的度數為 ;
類部分所對應扇形的圓心角的度數為 ;
(4)如果這所學校共有初中學生1500名,請你估算該校初中學生中對二戰歷史“非常了解”和“比較了解”的學生共有多少名?
【答案】(1)200;(2)見解析;(3)36°;(4)900名.
【解析】
(1)由圖①知A類人數為30,由圖②知A類人數占15%,即可求出抽查的總人數;
(2)由(1)可知抽查的總人數,根據圖②知C類人數占30%,求出C類人數,即可將條形統計圖補充完整;
(3)求出D類人數所占比例,即可求出圓心角的度數;
(4)求出樣本中A、B類總共占的比例,用樣本估計總體的思想計算即可.
解:(1)30÷15%=200(名),
即一共抽查了200名學生;
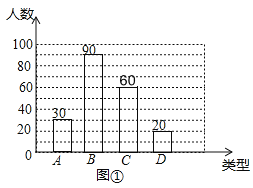
(2)C類人數為:200×30%=60(名),
條形統計圖如圖所示:
(3)![]() ,
,
即扇形統計圖中![]() 類部分所對應扇形的圓心角的度數為
類部分所對應扇形的圓心角的度數為![]() ;
;
(4)1500×![]() =900(名),
=900(名),
答:估計該校初中學生中對二戰歷史“非常了解”和“比較了解”的學生共有900名.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,我們定義直線y=ax-a為拋物線y=ax2+bx+c(a、b、c為常數,a≠0)的“衍生直線”;有一個頂點在拋物線上,另有一個頂點在y軸上的三角形為其“衍生三角形”.已知拋物線![]() 與其“衍生直線”交于A、B兩點(點A在點B的左側),與x軸負半軸交于點C.
與其“衍生直線”交于A、B兩點(點A在點B的左側),與x軸負半軸交于點C.

(1)填空:該拋物線的“衍生直線”的解析式為 ,點A的坐標為 ,點B的坐標為 ;
(2)如圖,點M為線段CB上一動點,將△ACM以AM所在直線為對稱軸翻折,點C的對稱點為N,若△AMN為該拋物線的“衍生三角形”,求點N的坐標;
(3)當點E在拋物線的對稱軸上運動時,在該拋物線的“衍生直線”上,是否存在點F,使得以點A、C、E、F為頂點的四邊形為平行四邊形?若存在,請直接寫出點E、F的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
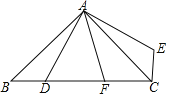
【題目】如圖,在△ABC中,∠BAC=90°,AB=AC,點D是BC上一動點,連接AD,過點A作AE⊥AD,并且始終保持AE=AD,連接CE.
(1)求證:△ABD≌△ACE;
(2)若AF平分∠DAE交BC于F,探究線段BD,DF,FC之間的數量關系,并證明;
(3)在(2)的條件下,若BD=3,CF=4,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
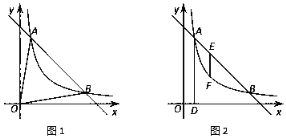
【題目】如圖1,點A(m,6),B(6,1)在反比例函數圖象上,作直線AB,連接OA、OB.
(1)求反比例函數的表達式和m的值;
(2)求△AOB的面積;
(3)如圖2,E是線段AB上一點,作AD⊥x軸于點D,過點E作x軸的垂線,交反比例函數圖象于點F,若EF=![]() AD,求出點E的坐標.
AD,求出點E的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 如圖1,以△ABC的邊AB為直徑作⊙O,交AC于點E,BD平分∠ABE交AC于F,交圓O于點D,且∠BDE=∠CBE.
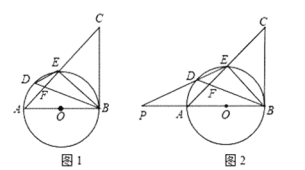
(1)求證:BC是⊙O的切線;
(2)如圖2,延長ED交直線AB于點P,若 PA=AO,DE=2,求![]() 的值及AO的長.
的值及AO的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在三角形![]() 中,
中,![]() ,
,![]() 和
和![]() 關于
關于![]() 對稱
對稱
(1)將圖1中的![]() 以
以![]() 為旋轉中心,逆時針方向旋轉角
為旋轉中心,逆時針方向旋轉角![]() ,使
,使![]() ,得到如圖2所示的
,得到如圖2所示的![]() ,分別延長
,分別延長![]() 和
和![]() 交于點
交于點![]() ,則四邊形
,則四邊形![]() 的形狀是 ;
的形狀是 ;
(2)將圖1中的![]() 以
以![]() 為旋轉中心,按逆時針方向旋轉角
為旋轉中心,按逆時針方向旋轉角![]() ,使
,使![]() ,得到如圖3所示的
,得到如圖3所示的![]() ,連接
,連接![]() 和
和![]() ,得到四邊形
,得到四邊形![]() ,請判斷四邊形
,請判斷四邊形![]() 的形狀,并說明理由;
的形狀,并說明理由;
(3)如圖3中,![]() ,將
,將![]() 沿著射線
沿著射線![]() 方向平移
方向平移![]() ,得到
,得到![]() ,連接
,連接![]() ,使四邊形
,使四邊形![]() 恰好為正方形,請直接寫出a的值.
恰好為正方形,請直接寫出a的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩車分別從A、B兩地同時出發,在同一條公路上,勻速行駛,相向而行,到兩車相遇時停止.甲車行駛一段時間后,因故停車0.5小時,故障解除后,繼續以原速向B地行駛,兩車之間的路程y(千米)與出發后所用時間x(小時)之間的函數關系如圖所示.

(1)求甲、乙兩車行駛的速度V甲、V乙.
(2)求m的值.
(3)若甲車沒有故障停車,求可以提前多長時間兩車相遇.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 與直線
與直線![]() 有兩個不同的交點.下列結論:①
有兩個不同的交點.下列結論:①![]() ;②當
;②當![]() 時,
時,![]() 有最小值
有最小值![]() ;③方程
;③方程![]() 有兩個不等實根;④若連接這兩個交點與拋物線的頂點,恰好是一個等腰直角三角形,則
有兩個不等實根;④若連接這兩個交點與拋物線的頂點,恰好是一個等腰直角三角形,則![]() ;其中正確的結論的個數是( )
;其中正確的結論的個數是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:∠BAC.
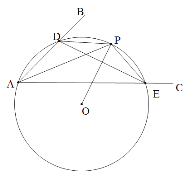
(1)如圖,在平面內任取一點O;
(2)以點O為圓心,OA為半徑作圓,交射線AB于點D,交射線AC于點E;
(3)連接DE,過點O作線段DE的垂線交⊙O于點P;
(4)連接AP,DP和PE.根據以上作圖過程及所作圖形,下列四個結論中:
①△ADE是⊙O的內接三角形; ② ![]() ;
;
③ DE=2PE; ④ AP平分∠BAC.
所有正確結論的序號是______________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com