
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),與
的左側),與![]() 軸相交于點
軸相交于點![]() ,頂點為
,頂點為![]() ,連接
,連接![]() ,與拋物線的對稱軸交于點
,與拋物線的對稱軸交于點![]() ,點
,點![]() 為線段
為線段![]() 上的一個動點(
上的一個動點(![]() 不與
不與![]() ,
,![]() 兩點重合),過點
兩點重合),過點![]() 作
作![]() 軸的垂線交拋物線于點
軸的垂線交拋物線于點![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]()
(1)當![]() 為何值時,四邊形
為何值時,四邊形![]() 為平行四邊形;
為平行四邊形;
(2)設![]() 的面積為
的面積為![]() ,求
,求![]() 的最大值.
的最大值.

【答案】(1)當![]() 時,四邊形
時,四邊形![]() 為平行四邊形;(2)
為平行四邊形;(2)![]() 的最大值為
的最大值為![]() .
.
【解析】
(1)對于拋物線解析式,令x=0求出y的值確定出C的坐標,令y=0求出x的值,確定出A與B坐標,根據B與C坐標,利用待定系數法確定出直線BC解析式,進而表示出E與P坐標,根據拋物線解析式確定出D與F坐標,表示出PF,利用平行四邊形的判定方法確定出m的值即可;
(2)先求出OB的長,△BCF面積![]() ,列出S關于m的二次函數解析式,利用二次函數性質確定出S的最大值即可.
,列出S關于m的二次函數解析式,利用二次函數性質確定出S的最大值即可.
(1)對于拋物線![]() ,
,
![]() 頂點
頂點![]()
令![]() ,得到
,得到![]() ;
;
令![]() ,得到
,得到![]() ,即
,即![]() ,
,
解得:![]() 或
或![]() ,
,
則![]() ,
,![]() ,
,![]() ,拋物線對稱軸為直線
,拋物線對稱軸為直線![]() ;
;
設直線![]() 的函數解析式為
的函數解析式為![]() ,
,
把![]() ,
,![]() 分別代入得:
分別代入得:![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 直線
直線![]() 的解析式為
的解析式為![]() ,
,
當![]() 時,
時,![]() ,
,
![]() ,
,
![]() ,
,
![]() 軸,
軸,
![]() ,
,![]() ,
,
![]() 線段
線段![]() ,
,
連接![]() ,由
,由![]() ,得到當
,得到當![]() 時,四邊形
時,四邊形![]() 為平行四邊形,
為平行四邊形,
由![]() ,得到
,得到![]() 或
或![]() (不合題意,舍去),
(不合題意,舍去),
當![]() 時,四邊形
時,四邊形![]() 為平行四邊形;
為平行四邊形;
(2)![]() ,
,
![]() ,
,
![]() ,
,
則當![]() 時,
時,![]() 取得最大值為
取得最大值為![]() .
.



 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,CD是斜邊AB上的中線,那么下列結論錯誤的是( )
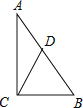
A.∠A+∠DCB=90°B.∠ADC= 2∠BC. AB=2CDD. BC=CD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某單位要將一份宣傳資料進行批量印刷.在甲印刷廠,在收取100元制版費的基礎上,每份收費0.5元;在乙印刷廠,在收取40元側版費的基礎上,每份收費0.7元.設該單位要印刷此宣傳資料![]() 份(
份(![]() 為正整數).
為正整數).
(Ⅰ)根據題意,填寫下表:
印劇數量(份) | 150 | 250 | 350 | 450 | … |
甲印刷廠收費(元) | 175 | ① | 275 | ② | … |
乙印刷廠收費(元) | 145 | 215 | ③ | 355 | … |
(Ⅱ)設在甲印刷廠收費![]() 元,在乙印刷廠收費
元,在乙印刷廠收費![]() 元,分別寫出
元,分別寫出![]() ,
,![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(Ⅲ)當![]() 時,在哪家印刷廠花費少?請說明理由.
時,在哪家印刷廠花費少?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
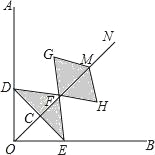
【題目】如圖,在Rt∠AOB的平分線ON上依次取點C,F,M,過點C作DE⊥OC,分別交OA,OB于點D,E,以FM為對角線作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,設OC=x,圖中陰影部分面積為y,則y與x之間的函數關系式是( )
A. y=![]() B. y=
B. y=![]() C. y=2
C. y=2![]() D. y=3
D. y=3![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,等邊三角形![]() 的邊長為2,
的邊長為2,![]() 是
是![]() 邊上的任一點(與
邊上的任一點(與![]() 不重合),設
不重合),設![]() ,連接
,連接![]() ,以
,以![]() 為邊向兩側作等邊三角形
為邊向兩側作等邊三角形![]() 和等邊三角形
和等邊三角形![]() ,分別與邊
,分別與邊![]() 交于點
交于點![]() .
.
(1)求證:![]() ;
;
(2)求四邊形![]() 與△ABC重疊部分的面積
與△ABC重疊部分的面積![]() 與
與![]() 之間的函數關系式及
之間的函數關系式及![]() 的最小值;
的最小值;
(3)如圖②,連接![]() ,分別與邊
,分別與邊![]() 交于點
交于點![]() .當
.當![]() 為何值時,
為何值時,![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】筆直的海岸線上依次有A,B,C三個港口,甲船從A港口出發,沿海岸線勻速駛向C港口,1小時后乙船從B港口出發,沿海岸線勻速駛向A港口,兩船同時到達目的地.甲船的速度是乙船的1.25倍,甲、乙兩船與B港口的距離y(km)與甲船行駛時間x(h)之間的函數關系如圖所示.給出下列說法:①A,B港口相距400km;②甲船的速度為100km/h;③B,C港口相距200km;④乙船出發4h時,兩船相距220km.其中正確的個數是( )
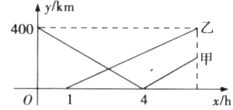
A.4B.3C.2D.1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 經過點
經過點![]() ,
,![]() ,直線
,直線![]() :
:![]() 交
交![]() 軸于點
軸于點![]() ,且與拋物線交于
,且與拋物線交于![]() ,
,![]() 兩點,
兩點,![]() 為拋物線上一動點(不與
為拋物線上一動點(不與![]() ,
,![]() 重合).
重合).
(1)求拋物線的解析式;
(2)當點![]() 在直線
在直線![]() 下方時,過點
下方時,過點![]() 作
作![]() 軸交
軸交![]() 于點
于點![]() ,
,![]() 軸交
軸交![]() 于點
于點![]() ,求
,求![]() 的最大值.
的最大值.
(3)設![]() 為直線
為直線![]() 上的點,以
上的點,以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形能否構成平行四邊形?若能,求出點
為頂點的四邊形能否構成平行四邊形?若能,求出點![]() 的坐標;若不能,請說明理由.
的坐標;若不能,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com