
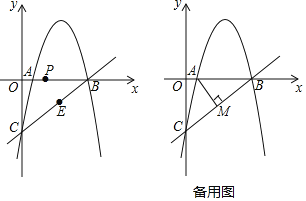
【題目】如圖,拋物線![]() 經過x軸上的點A(1,0)和點B及y軸上的點C,經過B、C兩點的直線為
經過x軸上的點A(1,0)和點B及y軸上的點C,經過B、C兩點的直線為![]() .
.
①求拋物線的解析式.
②點P從A出發,在線段AB上以每秒1個單位的速度向B運動,同時點E從B出發,在線段BC上以每秒2個單位的速度向C運動.當其中一個點到達終點時,另一點也停止運動.設運動時間為t秒,求t為何值時,△PBE的面積最大并求出最大值.
③過點A作![]() 于點M,過拋物線上一動點N(不與點B、C重合)作直線AM的平行線交直線BC于點Q.若點A、M、N、Q為頂點的四邊形是平行四邊形,求點N的橫坐標.
于點M,過拋物線上一動點N(不與點B、C重合)作直線AM的平行線交直線BC于點Q.若點A、M、N、Q為頂點的四邊形是平行四邊形,求點N的橫坐標.
【答案】①![]() ;②當
;②當![]() 時,△PBE的面積最大,最大值為
時,△PBE的面積最大,最大值為![]() ;③點N的橫坐標為:4或
;③點N的橫坐標為:4或![]() 或
或![]() .
.
【解析】
①點B、C在直線為![]() 上,則B(﹣n,0)、C(0,n),點A(1,0)在拋物線上,所以
上,則B(﹣n,0)、C(0,n),點A(1,0)在拋物線上,所以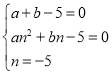 ,解得
,解得![]() ,
,![]() ,因此拋物線解析式:
,因此拋物線解析式:![]() ;
;
②先求出點P到BC的高h為![]() ,于是
,于是![]() ,當
,當![]() 時,△PBE的面積最大,最大值為
時,△PBE的面積最大,最大值為![]() ;
;
③由①知,BC所在直線為:![]() ,所以點A到直線BC的距離
,所以點A到直線BC的距離![]() ,過點N作x軸的垂線交直線BC于點P,交x軸于點H.設
,過點N作x軸的垂線交直線BC于點P,交x軸于點H.設![]() ,則
,則![]() 、
、![]() ,易證△PQN為等腰直角三角形,即
,易證△PQN為等腰直角三角形,即![]() ,
,![]() ,Ⅰ.
,Ⅰ.![]() ,所以
,所以![]() 解得
解得![]() (舍去),
(舍去),![]() ,Ⅱ.
,Ⅱ.![]() ,
,![]() 解得
解得![]() ,
,![]() (舍去),Ⅲ.
(舍去),Ⅲ.![]() ,
,![]() ,解得
,解得![]() (舍去),
(舍去),![]() .
.
解:①∵點B、C在直線為![]() 上,
上,
∴B(﹣n,0)、C(0,n),
∵點A(1,0)在拋物線上,
∴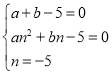 ,
,
∴![]() ,
,![]() ,
,
∴拋物線解析式:![]() ;
;
②由題意,得,
![]() ,
,![]() ,
,
由①知,![]() ,
,
∴點P到BC的高h為![]() ,
,
∴![]() ,
,
當![]() 時,△PBE的面積最大,最大值為
時,△PBE的面積最大,最大值為![]() ;
;
③由①知,BC所在直線為:![]() ,
,
∴點A到直線BC的距離![]() ,
,
過點N作x軸的垂線交直線BC于點P,交x軸于點H.
設![]() ,則
,則![]() 、
、![]() ,
,
易證△PQN為等腰直角三角形,即![]() ,
,
∴![]() ,
,
Ⅰ.![]() ,
,
∴![]()
解得![]() ,
,![]() ,
,
∵點A、M、N、Q為頂點的四邊形是平行四邊形,
∴![]() ;
;
Ⅱ.![]() ,
,
∴![]()
解得![]() ,
,![]() ,
,
∵點A、M、N、Q為頂點的四邊形是平行四邊形,
![]() ,
,
∴![]() ,
,
Ⅲ.![]() ,
,
∴![]() ,
,
解得![]() ,
,![]() ,
,
∵點A、M、N、Q為頂點的四邊形是平行四邊形,
![]() ,
,
∴![]() ,
,
綜上所述,若點A、M、N、Q為頂點的四邊形是平行四邊形,點N的橫坐標為:4或![]() 或
或![]() .
.


 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:初中數學 來源: 題型:
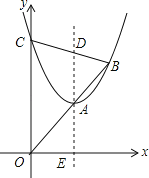
【題目】如圖,拋物線y=x2+bx+c(c>0)與y軸交于點C,頂點為A,拋物線的對稱軸交x軸于點E,交BC于點D,tan∠AOE=![]() .直線OA與拋物線的另一個交點為B.當OC=2AD時,c的值是_____.
.直線OA與拋物線的另一個交點為B.當OC=2AD時,c的值是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某電信公司提供了A,B兩種方案的移動通訊費用y(元)與通話時間x(元)之間的關系,則下列結論中正確的有( )
(1)若通話時間少于120分,則A方案比B方案便宜20元;
(2)若通話時間超過200分,則B方案比A方案便宜12元;
(3)若通訊費用為60元,則B方案比A方案的通話時間多;
(4)若兩種方案通訊費用相差10元,則通話時間是145分或185分.

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在下列10×10的網格中,橫、縱坐標均為整數的點叫做格點,例如A(3,0),B(4,3)都是格點.將△AOB繞點O順時針旋轉90°得到△COD(點A,B的對應點分別為點C,D).
(1)作出△COD;
(2)下面僅用無刻度的直尺畫△AOD的內心I,操作如下:
第一步:在x軸上找一格點E,連接DE,使OE=OD;
第二步:在DE上找一點F,連接OF,使OF平分∠AOD;
第三步:找格點G,得到正方形OAGC,連接AC,則AC與OF的交點I是△OAD的內心.
請你按步驟完成作圖,并直接寫出E,F,I三點的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在半徑為5的⊙O中,弦AB=8,P是弦AB所對的優弧上的動點,連接AP,過點A作AP的垂線交射線PB于點C,當△PAB是等腰三角形時,線段BC的長為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】吉祥超市準備購進甲、乙兩種綠色袋裝食品共800袋.甲、乙兩種綠色袋裝食品的進價和售價如表.已知:用2000元購進甲種袋裝食品的數量與用1600元購進乙種袋裝食品的數量相同.
甲 | 乙 | |
進價(元/袋) | m | m﹣2 |
售價(元/袋) | 20 | 13 |
(1)求m的值;
(2)假如購進的甲、乙兩種綠色袋裝食品全部賣出,所獲總利潤不少于5200元,且不超過5280元,問該超市有幾種進貨方案?(利潤=售價﹣進價)
查看答案和解析>>
科目:初中數學 來源: 題型:
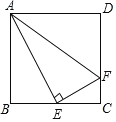
【題目】如圖,在正方形ABCD中,E是BC的中點,F是CD上一點,AE⊥EF.有下列結論:①∠BAE=30°;②射線FE是∠AFC的角平分線;③AE2=ADAF;④AF=AB+CF.其中正確結論為是______.(填寫所有正確結論的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,AB=AC,把△ABC繞A點沿順時針方向旋轉得到△ADE,連接BD,CE交于點F.

(1)求證:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,當四邊形ADFC是菱形時,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】課外閱讀是提高學生素養的重要途徑.某中學為了了解全校學生課外閱讀情況,隨機抽查了200名學生,統計他們平均每天課外閱讀時間(小時).根據每天課外閱讀時間的長短分為A,B,C.D四類,下面是根據所抽查的人數繪制的兩幅不完整的統計圖表,請根據圖中提供的信息,解答下面的問題:
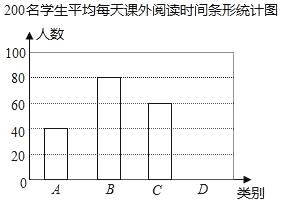
200名學生平均每天課外閱讀時間統計表
類別 | 時間t(小時) | 人數 |
A | t<0.5 | 40 |
B | 0.5≤t<1 | 80 |
C | 1≤t<1.5 | 60 |
D | t≥1.5 | a |
(1)求表格中a的值,并在圖中補全條形統計圖:
(2)該校現有1800名學生,請你估計該校共有多少名學生課外閱讀時間不少于1小時?
(3)請你根據上述信息對該校提出相應的建議
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com