
【題目】如圖1,已知拋物線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,與
,與![]() 軸相交于點
軸相交于點![]() 和點
和點![]() ,點
,點![]() 在點
在點![]() 的右側,點
的右側,點![]() 的坐標為
的坐標為![]() ,將線段
,將線段![]() 沿
沿![]() 軸的正方向平移
軸的正方向平移![]() 個單位后得到線段
個單位后得到線段![]() .
.
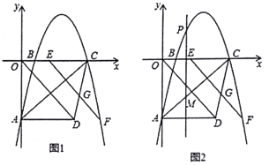
(1)當![]() ______時,點
______時,點![]() 或點
或點![]() 正好移動到拋物線上;
正好移動到拋物線上;
(2)當點![]() 正好移動到拋物線上,
正好移動到拋物線上,![]() 與
與![]() 相交于點
相交于點![]() 時,求
時,求![]() 點坐標;
點坐標;
(3)如圖2,若點![]() 是
是![]() 軸上方拋物線上一動點,過點
軸上方拋物線上一動點,過點![]() 作平行于
作平行于![]() 軸的直線交
軸的直線交![]() 于點
于點![]() ,探索是否存在點
,探索是否存在點![]() ,使線段
,使線段![]() 長度有最大值?若存在,直接寫出點
長度有最大值?若存在,直接寫出點![]() 的坐標和
的坐標和![]() 長度的最大值;若不存在,請說明理由.
長度的最大值;若不存在,請說明理由.
【答案】(1)1或2或5;(2)點![]() ;(3)存在點
;(3)存在點![]() ,使線段
,使線段![]() 長度有最大值為5.
長度有最大值為5.
【解析】
(1)分點E與點B重合,點E與點C重合,點F在拋物線上三種情況討論,可求n的值;
(2)由題意可求直線EF解析式,直線CD解析式,即可求點G坐標;
(3)由題意可求直線AC解析式,設點P(t,-![]() t2+
t2+![]() t-4),則點M(t,
t-4),則點M(t,![]() t-4),則可用t表示PM的長度,根據二次函數的性質可求點P的坐標.
t-4),則可用t表示PM的長度,根據二次函數的性質可求點P的坐標.
解:(1)∵拋物線![]() 與x軸相交于B和點C
與x軸相交于B和點C
∴![]()
解得:x1=1,x2=5
∴點B(1,0),點C(5,0)
當點E與點B重合,則n=1,
當點E與點C重合,則n=5
當點F在拋物線上,則![]()
解得:x1=0(不合題意舍去),x2=6
∴F(6,-4)
∴n=6-4=2
故答案為:1或2或5;
(2)∵點![]() 正好移動到拋物線上
正好移動到拋物線上
∴![]()
∴點![]() 坐標為
坐標為![]()
設直線![]() 解析式為
解析式為![]() ,把點
,把點![]() ,點
,點![]() 代入解析式得
代入解析式得
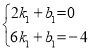 ,解得
,解得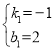
∴直線![]() 解析式為:
解析式為:![]()
設直線CD解析式為![]() ,把點
,把點![]() ,點
,點![]() 代入解析式得
代入解析式得
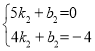 ,解得
,解得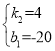
∴直線![]() 解析式
解析式![]()
∵![]() 與
與![]() 相交于點
相交于點![]() ,設點
,設點![]()
![]() ,解得:
,解得: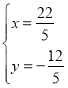
∴點![]() ,
,
(3)∵拋物線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,
,
∴當![]() 時,
時,![]()
∴點![]()
∵點![]() ,點
,點![]()
∴直線![]() 解析式:
解析式:![]() ,
,
設點![]() ,則點
,則點![]() ,
,
∴![]() ,
,
∴當![]() 時,
時,![]() 的最大值為5
的最大值為5
∴點![]() 坐標為
坐標為![]() ,
,
∴存在點![]() ,使線段
,使線段![]() 長度有最大值為5.
長度有最大值為5.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】疫情防控形勢下,人們在外出時都應戴上口罩以保護自己免受新型冠狀病毒感染.某藥店用4000元購進若干包一次性醫用口罩,很快售完,該店又用![]() 元錢購進第二批這種口罩,所進的包數比第一批多
元錢購進第二批這種口罩,所進的包數比第一批多![]() ,每包口罩的進價比第一批每包口罩的進價多
,每包口罩的進價比第一批每包口罩的進價多![]() 元,請解答下列問題:
元,請解答下列問題:

![]() 求購進的第一批醫用口罩有多少包;
求購進的第一批醫用口罩有多少包;
![]() 政府采取措施,在這兩批醫用口罩的銷售中,售價保持了一致.若售完這兩批口罩的總利潤不高于
政府采取措施,在這兩批醫用口罩的銷售中,售價保持了一致.若售完這兩批口罩的總利潤不高于![]() 元錢,那么藥店銷售該口罩每包的最高售價是多少元?
元錢,那么藥店銷售該口罩每包的最高售價是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
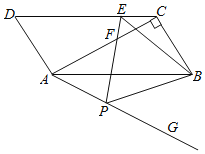
【題目】如圖,在ABCD中,對角線AC⊥BC,∠BAC=30°,BC=2![]() ,在AB邊的下方作射線AG,使得∠BAG=30°,E為線段DC上一個動點,在射線AG上取一點P,連接BP,使得∠EBP=60°,連接EP交AC于點F,在點E的運動過程中,當∠BPE=60°時,則AF=_____.
,在AB邊的下方作射線AG,使得∠BAG=30°,E為線段DC上一個動點,在射線AG上取一點P,連接BP,使得∠EBP=60°,連接EP交AC于點F,在點E的運動過程中,當∠BPE=60°時,則AF=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
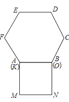
【題目】已知正方形![]() 和正六邊形
和正六邊形![]() 邊長均為1,如圖所示,把正方形放置在正六邊形外,使
邊長均為1,如圖所示,把正方形放置在正六邊形外,使![]() 邊與
邊與![]() 邊重合,按下列步驟操作:將正方形在正六邊形外繞點
邊重合,按下列步驟操作:將正方形在正六邊形外繞點![]() 逆時針旋轉,使
逆時針旋轉,使![]() 邊與
邊與![]() 邊重合,完成第一次旋轉;再繞點
邊重合,完成第一次旋轉;再繞點![]() 逆時針旋轉,使
逆時針旋轉,使![]() 邊與
邊與![]() 邊重合,完成第二次旋轉;此時點
邊重合,完成第二次旋轉;此時點![]() 經過路徑的長為___________.若按此方式旋轉,共完成六次,在這個過程中點
經過路徑的長為___________.若按此方式旋轉,共完成六次,在這個過程中點![]() ,
,![]() 之間距離的最大值是______.
之間距離的最大值是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線y=ax2+2ax+c(a≠0)與x軸交于點A,B(1,0)兩點,與y軸交于點C,且OA=OC.
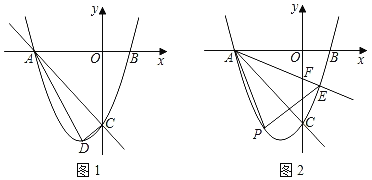
(1)求拋物線的解析式;
(2)點D是拋物線頂點,求△ACD的面積;
(3)如圖2,射線AE交拋物線于點E,交y軸的負半軸于點F(點F在線段AE上),點P是直線AE下方拋物線上的一點,S△ABE=![]() ,求△APE面積的最大值和此動點P的坐標.
,求△APE面積的最大值和此動點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解不等式組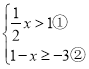
請結合題意,完成本題解答.
(1)解不等式①,得_________________;
(2)解不等式②,得:_________________;
(3)原不等式組的解集為_________________;
(4)把不等式組的解集在數軸上表示出來.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
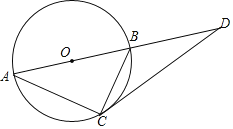
【題目】如圖,已知AB是⊙O的直徑,DC與⊙O相切于點C,交AB的延長線于點D.
(1)求證:∠BAC=∠BCD;
(2)若BD=4,DC=6,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,反比例函數![]() (k>0)與一次函數
(k>0)與一次函數![]() 的圖象相交于兩點A(
的圖象相交于兩點A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),線段AB交y軸與C,當|
),線段AB交y軸與C,當|![]() -
-![]() |=2且AC = 2BC時,k、b的值分別為( )
|=2且AC = 2BC時,k、b的值分別為( )

A. k=![]() ,b=2 B. k=
,b=2 B. k=![]() ,b=1 C. k=
,b=1 C. k=![]() ,b=
,b=![]() D. k=
D. k=![]() ,b=
,b=![]()
【答案】D
【解析】∵AC=2BC,∴A點的橫坐標的絕對值是B點橫坐標絕對值的兩倍.∵點A、點B都在一次函數y=x+b的圖象上,∴設B(m, ![]() m+b),則A(-2m,-m+b),∵|
m+b),則A(-2m,-m+b),∵|![]() -
-![]() |=2,∴m-(-2m)=2,解得m=
|=2,∴m-(-2m)=2,解得m=![]() ,又∵點A、點B都在反比例函數
,又∵點A、點B都在反比例函數![]() 的圖象上,∴
的圖象上,∴![]() (
(![]() +b)=(-
+b)=(-![]() )×(-
)×(-![]() +b),解得b=
+b),解得b=![]() ,∴k=
,∴k=![]() ×(
×(![]() +
+![]() )=
)=![]() ,故選D.
,故選D.
【題型】單選題
【結束】
11
【題目】若點(4,m)在反比例函數![]() (x≠0)的圖象上,則m的值是 .
(x≠0)的圖象上,則m的值是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com