
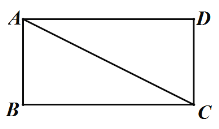
【題目】如圖,矩形ABCD中,AD>AB,連接AC,將線段AC繞點(diǎn)A順時(shí)針旋轉(zhuǎn)90得到線段AE,平移線段AE得到線段DF(點(diǎn)A與點(diǎn)D對(duì)應(yīng),點(diǎn)E與點(diǎn)F對(duì)應(yīng)),連接BF,分別交直線AD,AC于點(diǎn)G,M,連接EF.
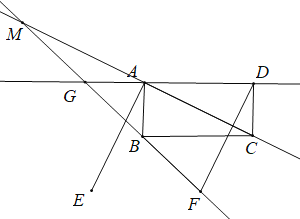
(1) 依題意補(bǔ)全圖形;
(2) 求證:EG⊥AD;
(3) 連接EC,交BF于點(diǎn)N,若AB=2,BC=4,設(shè)MB=a,NF=b,試比較![]() 與
與![]() 之間的大小關(guān)系,并證明.
之間的大小關(guān)系,并證明.
【答案】(1)見解析;(2)見解析;(3)![]() <
<![]() ,理由見解析.
,理由見解析.
【解析】
(1)根據(jù)題目要求作出圖形即可;
(2)連EF,EG,延長AB交EF于點(diǎn)H,先依據(jù)矩形與平行線的性質(zhì),等角的余角相等,旋轉(zhuǎn)的性質(zhì),得到![]() ≌
≌![]() (AAS),依據(jù)全等的性質(zhì)及等量代換可得
(AAS),依據(jù)全等的性質(zhì)及等量代換可得![]() ,結(jié)合依據(jù)相似的判定與性質(zhì),得到
,結(jié)合依據(jù)相似的判定與性質(zhì),得到![]() ,再依據(jù)SAS可證明
,再依據(jù)SAS可證明![]() ≌
≌![]() ,依據(jù)全等的性質(zhì)得到
,依據(jù)全等的性質(zhì)得到![]() ,即EG⊥AD;
,即EG⊥AD;
(3)依據(jù)勾股定理求出![]() ,依據(jù)平行線分線段成比例可分別證
,依據(jù)平行線分線段成比例可分別證![]() ∽
∽![]() ,
,![]() ∽
∽![]() ,
,![]() ∽
∽![]() ,依據(jù)相似三角形的性質(zhì)得到
,依據(jù)相似三角形的性質(zhì)得到![]() 、
、![]() 、
、![]() 、
、![]() ,即可求出
,即可求出![]() =
=![]() =9+5
=9+5![]() <
<![]() .
.
解:(1)補(bǔ)全圖形如下:
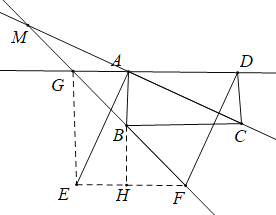
(2)連EF,EG,延長AB交EF于點(diǎn)H,設(shè)![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() ,
,![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∵矩形ABCD,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
又∵![]() ,
,
∴![]() ≌
≌![]() (AAS),
(AAS),
∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() (SAS),
(SAS),
∴![]() ,
,
∴EG⊥AD;
(3) 當(dāng)AB=2,BC=4,MB=a,NF=b時(shí),![]() <
<![]() ,理由如下:
,理由如下:
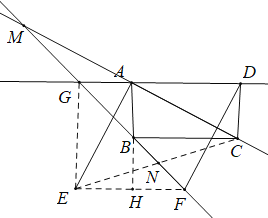
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,
∵![]()
![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() =
=![]() =9+5
=9+5![]() <
<![]() .
.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
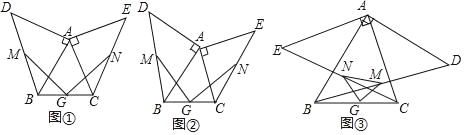
【題目】(1)操作發(fā)現(xiàn):如圖①,小明畫了一個(gè)等腰三角形ABC,其中AB=AC,在△ABC的外側(cè)分別以AB,AC為腰作了兩個(gè)等腰直角三角形ABD,ACE,分別取BD,CE,BC的中點(diǎn)M,N,G,連接GM,GN.小明發(fā)現(xiàn)了:線段GM與GN的數(shù)量關(guān)系是__________;位置關(guān)系是__________.
(2)類比思考:
如圖②,小明在此基礎(chǔ)上進(jìn)行了深入思考.把等腰三角形ABC換為一般的銳角三角形,其中AB>AC,其它條件不變,小明發(fā)現(xiàn)的上述結(jié)論還成立嗎?請(qǐng)說明理由.
(3)深入研究:
如圖③,小明在(2)的基礎(chǔ)上,又作了進(jìn)一步的探究.向△ABC的內(nèi)側(cè)分別作等腰直角三角形ABD,ACE,其它條件不變,試判斷△GMN的形狀,并給與證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)以下信息,解答下列問題.

(1)小華同學(xué)設(shè)乙型機(jī)器人每小時(shí)搬運(yùn)xkg產(chǎn)品,可列方程為 .
小惠同學(xué)設(shè)甲型機(jī)器人搬運(yùn)800kg所用時(shí)間為y小時(shí),可列方程為 .
(2)請(qǐng)你按照(1)中小華同學(xué)的解題思路,寫出完整的解答過程.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平行四邊形ABCD中,對(duì)角線AC,BD交于點(diǎn)O,E是邊AD上的一個(gè)動(dòng)點(diǎn)(與點(diǎn)A,D不重合),連接EO并延長,交BC于點(diǎn)F,連接BE,DF.下列說法:
① 對(duì)于任意的點(diǎn)E,四邊形BEDF都是平行四邊形;
② 當(dāng)∠ABC>90°時(shí),至少存在一個(gè)點(diǎn)E,使得四邊形BEDF是矩形;
③ 當(dāng)AB<AD時(shí),至少存在一個(gè)點(diǎn)E,使得是四邊形BEDF是菱形;
④ 當(dāng)∠ADB=45°時(shí),至少存在一個(gè)點(diǎn)E,使得是四邊形BEDF是正方形.
所有正確說法的序號(hào)是:_________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
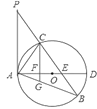
【題目】如圖,已知在![]() 中,
中,![]() 是
是![]() 邊上一點(diǎn),
邊上一點(diǎn),![]() ,
,![]() 是
是![]() 的外接圓,
的外接圓,![]() 是
是![]() 的直徑,且交
的直徑,且交![]() 于點(diǎn)
于點(diǎn)![]() .
.
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)過點(diǎn)![]() 作
作![]() ,垂足為點(diǎn)
,垂足為點(diǎn)![]() ,延長
,延長![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,若
,若![]() ,求
,求![]() 的長;
的長;
(3)在滿足(2)的條件下,若![]() ,
,![]() ,求
,求![]() 的半徑及
的半徑及![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】再讀教材:寬與長的比是![]() (約為0.618)的矩形叫作黃金矩形.黃金矩形給我們以協(xié)調(diào)、勻稱的美感,世界各國許多著名的建筑,為取得最佳的視覺效果,都采用了黃金矩形的設(shè)計(jì).下面,我們用寬為2的矩形紙片折疊黃金矩形(提示:
(約為0.618)的矩形叫作黃金矩形.黃金矩形給我們以協(xié)調(diào)、勻稱的美感,世界各國許多著名的建筑,為取得最佳的視覺效果,都采用了黃金矩形的設(shè)計(jì).下面,我們用寬為2的矩形紙片折疊黃金矩形(提示:![]() ).
).
第一步:在矩形紙片一端 ,利用圖1的方法折出一個(gè)正方形,然后把紙片展平;
第二步:如圖2,把這個(gè)正方形折成兩個(gè)相等的矩形,再把紙片展平;
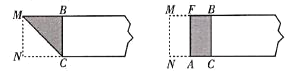
圖1 圖2
第三步:折出內(nèi)側(cè)矩形的對(duì)角線![]() ,并把
,并把![]() 折到圖3中所示的
折到圖3中所示的![]() 處;
處;
第四步:展平紙片,按照所得的點(diǎn)![]() 折出
折出![]() ,使
,使![]() ,則圖4中就會(huì)出現(xiàn)黃金矩形.
,則圖4中就會(huì)出現(xiàn)黃金矩形.
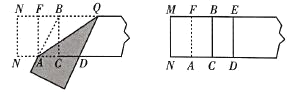
圖3 圖4
(1)在圖3中![]() _________ (保留根號(hào));
_________ (保留根號(hào));
(2)如圖3,則四邊形![]() 的形狀是_________;
的形狀是_________;
(3)在圖4中黃金矩形是_________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
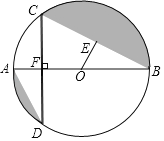
【題目】如圖,AB為⊙O直徑,OE⊥BC垂足為E,AB⊥CD垂足為F.
(1)求證:AD=2OE;
(2)若∠ABC=30°,⊙O的半徑為2,求兩陰影部分面積的和.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四邊形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果點(diǎn)P由B點(diǎn)出發(fā)沿BC方向向點(diǎn)C勻速運(yùn)動(dòng),同時(shí)點(diǎn)Q由A點(diǎn)出發(fā)沿AB方向向點(diǎn)B勻速運(yùn)動(dòng),它們的速度均為1cm/s,當(dāng)P點(diǎn)到達(dá)C點(diǎn)時(shí),兩點(diǎn)同時(shí)停止運(yùn)動(dòng),連接PQ,設(shè)運(yùn)動(dòng)時(shí)間為t s,解答下列問題:
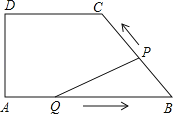
(1)當(dāng)t為何值時(shí),P,Q兩點(diǎn)同時(shí)停止運(yùn)動(dòng);
(2)設(shè)△PQB的面積為S,當(dāng)t為何值時(shí),S取得最大值,并求出最大值;
(3)當(dāng)△PQB為等腰三角形時(shí),求t的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com