
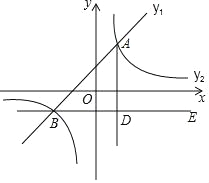
【題目】如圖,在平面直角坐標系中,一次函數y1=ax+b的圖象與反比例函數y2=![]() 的圖象交于點A(1,2)和B(﹣2,m).
的圖象交于點A(1,2)和B(﹣2,m).
(1)求一次函數和反比例函數的表達式;
(2)請直接寫出y1≥y2時x的取值范圍;
(3)過點B作BE∥x軸,AD⊥BE于點D,點C是直線BE上一點,若∠DAC=30°,求點C的坐標.
【答案】(1)反比例函數的解析式為y2=![]() ;一次函數解析式為y1=x+1.(2)當﹣2≤x<0或x≥1時,y1≥y2.(3)點C的坐標為(1﹣
;一次函數解析式為y1=x+1.(2)當﹣2≤x<0或x≥1時,y1≥y2.(3)點C的坐標為(1﹣![]() ,﹣1)或(1+
,﹣1)或(1+![]() ,﹣1).
,﹣1).
【解析】
(1)由點A的坐標,利用反比例函數圖象上點的坐標特征可求出k值,由點B的橫坐標利用反比例函數圖象上點的坐標特征可求出m值,進而可得出點B的坐標,根據點A,B的坐標,利用待定系數法即可求出一次函數解析式;
(2)觀察函數圖象,由兩函數圖象的上下位置關系結合兩交點的坐標,即可找出y1≥y2時x的取值范圍;
(3)由點A,B的縱坐標可得出AD的長度及點D的坐標,在Rt△ADC中,由∠DAC=30°可得出CD的長度,再結合點D的坐標即可求出點C的坐標.
(1)∵點A(1,2)在反比例函數y2=![]() 的圖象上,
的圖象上,
∴2=![]() ,
,
∴k=1×2=2,
∴反比例函數的解析式為y2=![]() .
.
∵點B(﹣2,m)在反比例函數y2=![]() 的圖象上,
的圖象上,
∴m=![]() =﹣1,
=﹣1,
∴點B的坐標為(﹣2,﹣1).
把A(1,2),B(﹣2,﹣1)代入y1=ax+b得:![]()
解得:![]()
∴一次函數解析式為y1=x+1.
(2)由函數圖象可知:當﹣2≤x<0或x≥1時,y1≥y2.
(3)由題意得:AD=2﹣(﹣1)=3,點D的坐標為(1,﹣1).
在Rt△ADC中,tan∠DAC=![]() ,即
,即![]() ,
,
解得:CD=![]() .
.
當點C在點D的左側時,點C的坐標為(1﹣![]() ,﹣1);
,﹣1);
當點C在點D的右側時,點C的坐標為(1+![]() ,﹣1).
,﹣1).
∴點C的坐標為(1﹣![]() ,﹣1)或(1+
,﹣1)或(1+![]() ,﹣1).
,﹣1).


 捷徑訓練檢測卷系列答案
捷徑訓練檢測卷系列答案 小夫子全能檢測系列答案
小夫子全能檢測系列答案科目:初中數學 來源: 題型:
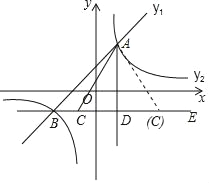
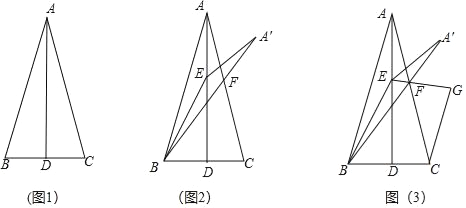
【題目】已知:AD是△ABC的高,且BD=CD.
(1)如圖1,求證:∠BAD=∠CAD;
(2)如圖2,點E在AD上,連接BE,將△ABE沿BE折疊得到△A′BE,A′B與AC相交于點F,若BE=BC,求∠BFC的大小;
(3)如圖3,在(2)的條件下,連接EF,過點C作CG⊥EF,交EF的延長線于點G,若BF=10,EG=6,求線段CF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
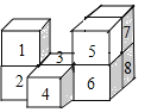
【題目】如圖,是用8個大小相同的小正方體搭成的幾何體,僅在該幾何體中取走一塊小正方體,使得到的新幾何體同時滿足兩個要求:(1)從正面看到的形狀和原幾何體從正面看到的形狀相同;(2)從左面看到的形狀和原幾何體從左面看到的形狀也相同.在不改變其它小正方體位置的前提下,可取走的小正方體的標號是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知△ABC中,∠ACB=90°,CA=CB,點D,E分別在CB,CA上,且CD=CE,連AD,BE,F為AD的中點,連CF.
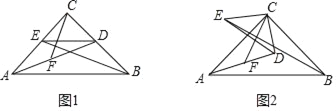
(1)求證:CF=![]() BE,且CF⊥BE;
BE,且CF⊥BE;
(2)將△CDE繞點C順時針旋轉一個銳角(如圖2),其它條件不變,此時(1)中的結論是否仍成立?并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校計劃一次性購買排球和籃球,每個籃球的價格比排球貴30元;購買2個排球和3個籃球共需340元.
(1)求每個排球和籃球的價格:
(2)若該校一次性購買排球和籃球共60個,總費用不超過3800元,且購買排球的個數少于39個.設排球的個數為m,總費用為y元.
①求y關于m的函數關系式,并求m可取的所有值;
②在學校按怎樣的方案購買時,費用最低?最低費用為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
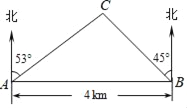
【題目】如圖,在一筆直的海岸線上有A、B兩個觀測點,B在A的正東方向,AB=4km.從A測得燈塔C在北偏東53°方向上,從B測得燈塔C在北偏西45°方向上,求燈塔C與觀測點A的距離(精確到0.1km).(參考數據:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】方格紙中每個小正方形的邊長都是單位1,△OAB在平面直角坐標系中的位置如圖所示.解答問題:
(1)請按要求對△ABO作如下變換:
①將△OAB向下平移2個單位,再向左平移3個單位得到△O1A1B1;
②以點O為位似中心,位似比為2:1,將△ABC在位似中心的異側進行放大得到△OA2B2.
(2)寫出點A1,A2的坐標: , ;
(3)△OA2B2的面積為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
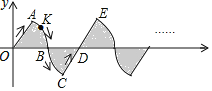
【題目】在平面直角坐標系xOy中,若干個半徑為1個單位長度,圓心角是![]() 的扇形按圖中的方式擺放,動點K從原點O出發,沿著“半徑OA
的扇形按圖中的方式擺放,動點K從原點O出發,沿著“半徑OA![]() 弧AB
弧AB![]() 弧BC
弧BC![]() 半徑CD
半徑CD![]() 半徑DE
半徑DE![]() ”的曲線運動,若點K在線段上運動的速度為每秒1個單位長度,在弧線上運動的速度為每秒
”的曲線運動,若點K在線段上運動的速度為每秒1個單位長度,在弧線上運動的速度為每秒![]() 個單位長度,設第n秒運動到點K,
個單位長度,設第n秒運動到點K,![]() 為自然數
為自然數![]() ,則
,則![]() 的坐標是____,
的坐標是____,![]() 的坐標是____
的坐標是____
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com