【題目】某農作物的生長率P與溫度t(℃)有如下關系：如圖1，當10≤t≤25時可近似用函數
刻畫；當25≤t≤37時可近似用函數
刻畫．
(1)求h的值．
(2)按照經驗，該作物提前上市的天數m(天)與生長率P滿足函數關系：
生長率P | 0.2 | 0.25 | 0.3 | 0.35 |
提前上市的天數m（天） | 0 | 5 | 10 | 15 |
①請運用已學的知識，求m關于P的函數表達式；
②請用含
的代數式表示m ；
(3)天氣寒冷，大棚加溫可改變農作物生長速度．在(2)的條件下，原計劃大棚恒溫20℃時，每天的成本為200元，該作物30天后上市時，根據市場調查：每提前一天上市售出(一次售完)，銷售額可增加600元．因此給大棚繼續加溫，加溫后每天成本w(元)與大棚溫度t(℃)之間的關系如圖2．問提前上市多少天時增加的利潤最大？并求這個最大利潤（農作物上市售出后大棚暫停使用）．
【答案】（1）
；（2）①
，②
；（3）當
時，提前上市20天，增加利潤的最大值為15000元.
【解析】
（1）根據
求出t=25時P的值，代入
即可；
（2）①由表格可知m與p的一次函數，用待定系數法求解即可；②分當
時與當
時兩種情況求解即可；
（3）分當
時與當
時兩種情況求出增加的利潤，然后比較即可.
（1）把t=25代入，得P=0.3，
把（25，0.3）的坐標代入
得或
，
.
（2）①由表格可知m與p的一次函數，設m=kp+b，由題意得
，
解之得
，
；
②當時，
，
當時，
.
；
（3）（Ⅰ）當時，
由
，
，得
.
增加利潤為
.
當
時，增加利潤的最大值為6000元.
（Ⅱ）當時，
.
增加利潤為
，
當時，增加利潤的最大值為15000元.
綜上所述，當時，提前上市20天，增加利潤的最大值為15000元.
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】某中學圍繞“哈爾濱市周邊五大名山,即:香爐山、鳳凰山、金龍山、帽兒山、二龍山,你最喜歡那一座山?(每名學生必選且只選一座山)的問題在全校范圍內隨機抽取了部分學生進行問卷調查,根據調查結果繪制了如圖的不完整的統計圖:
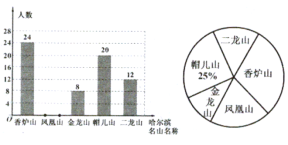
(1)求本次調查的樣本容量；
(2)求本次調查中,最喜歡鳳凰山的學生人數,并補全條形統計圖；
(3)若該中學共有學生1200人,請你估計該中學最喜歡香爐山的學生約有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了鼓勵市民節約用電，某市對居民用電實行“階梯收費”（總電費＝第一階梯電費+第二階梯電費）．規定：用電量不超過200度按第一階梯電價收費，超過200度的部分按第二階梯電價收費，如圖是張磊家2018年2月和3月所交電費的收據．
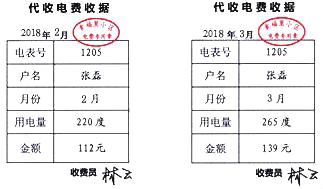
（1）該市規定的第一階梯電價和第二階梯電價單價分別為多少？
（2）張磊家4月份家庭支出計劃中電費為160元，他家最大用電量為多少度？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線y＝ax2﹣2ax+c(a＜0)的圖象過點A(3，m)．
(1)當a＝﹣1，m＝0時，求拋物線的頂點坐標_____；
(2)如圖，直線l：y＝kx+c(k＜0)交拋物線于B，C兩點，點Q(x，y)是拋物線上點B，C之間的一個動點，作QD⊥x軸交直線l于點D，作QE⊥y軸于點E，連接DE．設∠QED＝β，當2≤x≤4時，β恰好滿足30°≤β≤60°，a＝_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
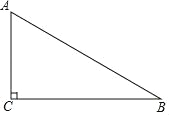
【題目】如圖，在Rt△ABC中，∠ACB＝90°．
（1）用尺規在邊BC上求作一點P，使PA＝PB（不寫作法，保留作圖痕跡）；
（2）連接AP，若AP平分∠CAB，求∠B的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1是2019年4月份的日歷，現用一長方形在日歷表中任意框出4個數(如圖2)，下列表示a，b，c，d之間關系的式子中不正確的是( )
A. a﹣d＝b﹣cB. a+c+2＝b+dC. a+b+14＝c+dD. a+d＝b+c
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一次函數
與反比例函數
的圖象交于A（1，4），B（4，n）兩點．
（1）求反比例函數和一次函數的解析式；
（2）直接寫出當x＞0時，
的解集．
（3）點P是x軸上的一動點，試確定點P并求出它的坐標，使PA+PB最小．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
