
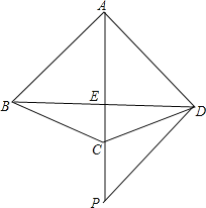
【題目】如圖,四邊形ABCD中,AB=AC=AD,AC平分∠BAD,點P是AC延長線上一點,且PD⊥AD.
(1)證明:∠BDC=∠PDC;
(2)若AC與BD相交于點E,AB=1,CE:CP=2:3,求AE的長.
【答案】(1)見解析(2)![]()
【解析】
(1)由三線合一可知AC⊥BD,然后利用等腰三角形的性質結合互余的定義得出∠BDC=∠PDC;
(2)首先過點C作CM⊥PD于點M,進而得出△CPM∽△APD,求出EC的長即可得出答案.
(1)證明:∵AB=AD,AC平分∠BAD,
∴AC⊥BD,
∴∠ACD+∠BDC=90°,
∵AC=AD,
∴∠ACD=∠ADC,
∴∠ADC+∠BDC=90°,
∵PD⊥AD,
∴∠ADC+∠PDC=90°,
∴∠BDC=∠PDC;
(2)解:過點C作CM⊥PD于點M,
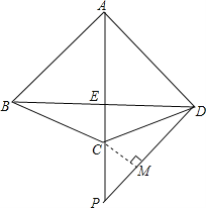
∵∠BDC=∠PDC,
∴CE=CM,
∵∠CMP=∠ADP=90°,∠P=∠P,
∴△CPM∽△APD,
∴![]() =
=![]() ,
,
設CM=CE=x,
∵CE:CP=2:3,
∴PC=![]() x,
x,
∵AB=AD=AC=1,
∴![]() =
=![]() ,
,
解得:x=![]() ,
,
故AE=1-![]() =
=![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 分別交y軸、x軸于A、B兩點,拋物線y=﹣x2+bx+c過A、B兩點.
分別交y軸、x軸于A、B兩點,拋物線y=﹣x2+bx+c過A、B兩點.
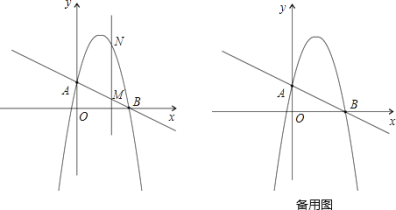
(1)求這個拋物線的解析式;
(2)作垂直x軸的直線x=t,在第一象限交直線AB于M,交這個拋物線于N.求當t取何值時,MN有最大值?最大值是多少?
(3)在(2)的情況下,以A、M、N、D為頂點作平行四邊形,求第四個頂點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一種實驗用軌道彈珠,在軌道上行駛5分鐘后離開軌道,前2分鐘其速度v(米/分)與時間t(分)滿足二次函數v=at2,后三分鐘其速度v(米/分)與時間t(分)滿足反比例函數關系,如圖,軌道旁邊的測速儀測得彈珠1分鐘末的速度為2米/分,求:
(1)二次函數和反比例函數的關系式.
(2)彈珠在軌道上行駛的最大速度.

【答案】(1)v=![]() (2<t≤5) (2)8米/分
(2<t≤5) (2)8米/分
【解析】分析:(1)由圖象可知前一分鐘過點(1,2),后三分鐘時過點(2,8),分別利用待定系數法可求得函數解析式;
(2)把t=2代入(1)中二次函數解析式即可.
詳解:(1)v=at2的圖象經過點(1,2),
∴a=2.
∴二次函數的解析式為:v=2t2,(0≤t≤2);
設反比例函數的解析式為v=![]() ,
,
由題意知,圖象經過點(2,8),
∴k=16,
∴反比例函數的解析式為v=![]() (2<t≤5);
(2<t≤5);
(2)∵二次函數v=2t2,(0≤t≤2)的圖象開口向上,對稱軸為y軸,
∴彈珠在軌道上行駛的最大速度在2秒末,為8米/分.
點睛:本題考查了反比例函數和二次函數的應用.解題的關鍵是從圖中得到關鍵性的信息:自變量的取值范圍和圖象所經過的點的坐標.
【題型】解答題
【結束】
24
【題目】閱讀材料:小胖同學發現這樣一個規律:兩個頂角相等的等腰三角形,如果具有公共的頂角的頂點,并把它們的底角頂點連接起來則形成一組旋轉全等的三角形.小胖把具有這個規律的圖形稱為“手拉手”圖形.如圖1,在“手拉手”圖形中,小胖發現若∠BAC=∠DAE,AB=AC,AD=AE,則BD=CE.
(1)在圖1中證明小胖的發現;
借助小胖同學總結規律,構造“手拉手”圖形來解答下面的問題:
(2)如圖2,AB=BC,∠ABC=∠BDC=60°,求證:AD+CD=BD;
(3)如圖3,在△ABC中,AB=AC,∠BAC=m°,點E為△ABC外一點,點D為BC中點,∠EBC=∠ACF,ED⊥FD,求∠EAF的度數(用含有m的式子表示).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有以下命題:
①如果線段d是線段a,b,c的第四比例項,則有![]() ;
;
②如果點C是線段AB的中點,那么AC是AB.BC的比例中項;
③如果點C是線段AB的黃金分割點,且AC>BC,那么AC是AB與BC的比例中項;
④如果點C是線段AB的黃金分割點,AC>BC,且AB=2,則AC=![]() -1.
-1.
其中正確的判斷有( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=90°,AB∥y軸,AB=3,反比例函數y=-![]() 的圖象經過點B,與AC交于點D,且CD=2AD,則點D的橫坐標是( )
的圖象經過點B,與AC交于點D,且CD=2AD,則點D的橫坐標是( )

A.-1B.-2C.-3D.-4
查看答案和解析>>
科目:初中數學 來源: 題型:
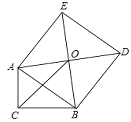
【題目】如圖,Rt△ABC中,∠C=90°,以斜邊AB為邊向外作正方形ABDE,且正方形對角線交于點O,連接OC,已知AC=![]() ,OC=
,OC=![]() ,則另一直角邊BC的長為__________.
,則另一直角邊BC的長為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點P是正方形ABCD邊AB上一點(不與A,B重合),連接PD并將線段PD繞點P順時針旋轉90°,得線段PE,連接BE,則∠CBE等于( )

A. 75° B. 60° C. 45° D. 30°
查看答案和解析>>
科目:初中數學 來源: 題型:
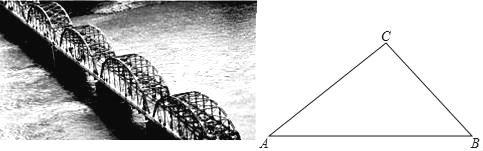
【題目】汾河孕育著世代的龍城子孫,而魅力汾河兩岸那“新外灘”的稱號,將太原人對汾河的愛表露無遺…貫穿太原的汾河,讓橋,也成為太原的文化符號,讓汾河兩岸,也成為繁華的必爭之地!北中環橋是世界上首座對稱五拱反對稱五跨非對稱斜拉索橋,2013年開工建設,當年實現全線竣工通車.這座橋造型現代,宛如一條騰飛巨龍.
小蕓和小剛分別在橋面上的A,B處,準備測量其中一座弧形鋼架拱梁頂部C處到橋面的距離AB=20m,小蕓在A處測得∠CAB=36°,小剛在B處測得∠CBA=43°,求弧形鋼架拱梁頂部C處到橋面的距離.(結果精確到0.1m)(參考數據sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin43°≈0.68,cos43°≈0.73,tan43°≈0.93)
查看答案和解析>>
科目:初中數學 來源: 題型:
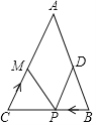
【題目】如圖,![]() ,
,![]() ,點D為
,點D為![]() 的中點,點P在邊
的中點,點P在邊![]() 上以每秒
上以每秒![]() 的速度由點B向點C運動,同時,點M在邊
的速度由點B向點C運動,同時,點M在邊![]() 上由點C向點A勻速運動.
上由點C向點A勻速運動.
(1)當點M的運動速度與點P的運動速度相同,經過1秒后,![]() 與
與![]() 是否全等?請說明理由;
是否全等?請說明理由;
(2)若點M的運動速度與點P的運動速度不相等,當點M的運動速度為多少時,能夠使![]() 與
與![]() 全等?
全等?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com