
【題目】如圖,在正方形ABCD中,點M在CD邊上,點N在正方形ABCD外部,且滿足∠CMN=90°,CM=MN.連接AN,CN,取AN的中點E,連接BE,AC,交于F點.
(1) ①依題意補全圖形;②求證:BE⊥AC.
(2)設AB=1,若點M沿著線段CD從點C運動到點D,則在該運動過程中,線段EN所掃過的面積為 (直接寫出答案).

【答案】(1)①見解析;②見解析;(2)![]()
【解析】
(1)①依照題意補全圖形即可;②連接CE,由正方形以及等腰直角三角形的性質可得出∠ACD=∠MCN=45°,從而得出∠ACN=90°,再根據直角三角形的性質以及點E為AN的中點即可得出AE=CE,由此即可得出B、E在線段AC的垂直平分線上,由此即可證得BE⊥AC;
(2)找出EN所掃過的圖形為四邊形DFCN.根據正方形以及等腰直角三角形的性質可得出BD∥CN,由此得出四邊形DFCN為梯形,再由AB=1,可算出線段CF、DF、CN的長度,利用梯形的面積公式即可得出結論.
(1)①依題意補全圖形,如圖1所示.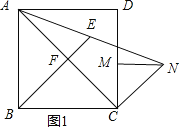
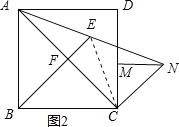
②證明:連接CE,如圖2所示.
∵四邊形ABCD是正方形,
∴∠BCD=90°,AB=BC,
∴∠ACB=∠ACD=![]() ∠BCD=45°,
∠BCD=45°,
∵∠CMN=90°,CM=MN,
∴∠MCN=45°,
∴∠ACN=∠ACD+∠MCN=90°.
∵在Rt△ACN中,點E是AN中點,
∴AE=CE=![]() AN.
AN.
∵AE=CE,AB=CB,
∴點B,E在AC的垂直平分線上,
∴BE垂直平分AC,
∴BE⊥AC.
(2)在點M沿著線段CD從點C運動到點D的過程中,線段EN所掃過的圖形為四邊形DFCN.
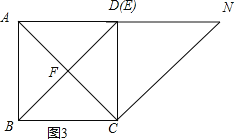
∵∠BDC=45°,∠DCN=45°,
∴BD∥CN,
∴四邊形DFCN為梯形.
∵AB=1,
∴CF=DF=![]() BD=
BD=![]() ,CN=
,CN=![]() ,
,
∴S梯形DFCN=![]() (DF+CN)CF=
(DF+CN)CF=![]() (
(![]() +
+![]() )×
)×![]() =
=![]() .
.
故答案為:![]() .
.


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:初中數學 來源: 題型:
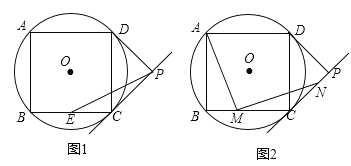
【題目】如圖,四邊形ABCD是⊙O的內接正方形,AB=4,PC、PD是⊙O的兩條切線,C、D為切點.
(1)如圖1,求⊙O的半徑;
(2)如圖1,若點E是BC的中點,連接PE,求PE的長度;
(3)如圖2,若點M是BC邊上任意一點(不含B、C),以點M為直角頂點,在BC的上方作∠AMN=90°,交直線CP于點N,求證:AM=MN.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠AEM+∠CDN=180°,EC平分∠AEF.

(1)若∠EFC=62°,求∠C的度數;
(2)若CE⊥MN,垂足為點E,求證:∠FDE=∠FED.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知直線
中,已知直線![]() 與反比例函數
與反比例函數![]() 的圖像交于點A,且點A的橫坐標為1,點B是x軸正半軸上一點,且
的圖像交于點A,且點A的橫坐標為1,點B是x軸正半軸上一點,且![]() ⊥
⊥![]() .
.
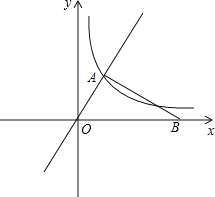
(1)求反比例函數的解析式;
(2)求點B的坐標;
(3)先在![]() 的內部求作點P,使點P到
的內部求作點P,使點P到![]() 的兩邊OA、OB的距離相等,且PA=PB.(不寫作法,保留作圖痕跡,在圖上標注清楚點P)
的兩邊OA、OB的距離相等,且PA=PB.(不寫作法,保留作圖痕跡,在圖上標注清楚點P)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知邊長為1的正方形ABCD中,P是對角線AC上的一個動點(與點A. C不重合),過點P作PE⊥PB,PE交射線DC于點E,過點E作EF⊥AC,垂足為點F,當點E落在線段CD上時(如圖),
(1)求證:PB=PE;
(2)在點P的運動過程中,PF的長度是否發生變化?若不變,試求出這個不變的值,若變化,試說明理由;

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠A=30°,直線a∥b,頂點C在直線b上,直線a交AB于點D,交AC于點E,若∠1=145°,則∠2的度數是( )

A.30°B.35°C.40°D.45°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C、E分別在直線AB、DF上,小華想知道∠ACE和∠DEC是否互補,但是他沒有帶量角器,只帶了一副三角板,于是他想了這樣一個辦法:首先連結CF,再找出CF的中點O,然后連結EO并延長EO和直線AB相交于點B,經過測量,他發現EO=BO,因此他得出結論:∠ACE和∠DEC互補,而且他還發現BC=EF.小華的想法對嗎?為什么?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠A=105°.
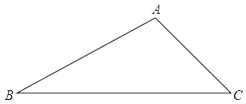
(1)試求作一點P,使得點P到B、C兩點的距離相等,并且到∠ABC兩邊的距離相等(尺規作圖,不寫作法,保留作圖痕跡).
(2)在(1)的條件下,若∠BCP=15°,則∠ACB的度數為 °.
查看答案和解析>>
科目:初中數學 來源: 題型:
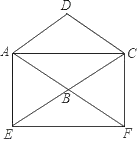
【題目】已知:如圖,菱形ABCD,分別延長AB,CB到點F,E,使得BF=BA,BE=BC,連接AE,EF,FC,CA.
(1)求證:四邊形AEFC為矩形;
(2)連接DE交AB于點O,如果DE⊥AB,AB=4,求DE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com