
【題目】解不等式組:![]() ;
;
請結合題意填空,完成本題的解答:
(ⅰ)解不等式(1),得_________;
(ⅱ)解不等式(2),得_________;
(ⅲ)把不等式(1)和(2)的解集在數軸上表示出來:
![]()
(ⅳ)原不等式的解集為:__________.
 課課優能力培優100分系列答案
課課優能力培優100分系列答案 優百分課時互動系列答案
優百分課時互動系列答案科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 與x軸分別交于
與x軸分別交于![]() ,
,![]() 兩點,與y軸交于點C.
兩點,與y軸交于點C.
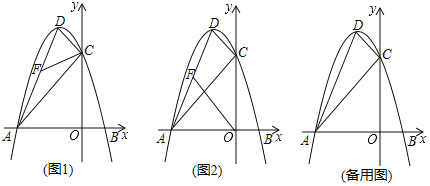
(1)求拋物線的表達式及頂點D的坐標;
(2)點F是線段AD上一個動點.
①如圖1,設![]() ,當k為何值時,
,當k為何值時,![]() .
.
②如圖2,以A,F,O為頂點的三角形是否與![]() 相似?若相似,求出點F的坐標;若不相似,請說明理由.
相似?若相似,求出點F的坐標;若不相似,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩座倉庫分別有農用車12輛和6輛.現在需要調往A縣10輛,需要調往B縣8輛,已知從甲倉庫調運一輛農用車到A縣和B縣的運費分別為40元和80元;從乙倉庫調運一輛農用車到A縣和B縣的運費分別為30元和50元.
(1)設乙倉庫調往A縣農用車x輛,先填好下表,再寫出總運費y關于x的函數關系式;

(2)若要求總運費不超過900元,問共有幾種調運方案?
(3)求出總運費最低的調運方案,最低運費是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
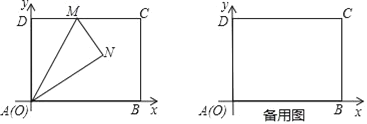
【題目】注意:為了使同學們更好地解答本題的第(Ⅱ)問,我們提供了一種分析問題的方法,你可以依照這個方法按要求完成本題的解答,也可以選用其他方法,按照解答題的一般要求進行解答即可.
如圖,將一個矩形紙片![]() ,放置在平面直角坐標系中,
,放置在平面直角坐標系中,![]() ,
,![]() ,
,![]() ,
,![]() 是邊
是邊![]() 上一點,將
上一點,將![]() 沿直線
沿直線![]() 折疊,得到
折疊,得到![]() .
.
(Ⅰ)當![]() 平分
平分![]() 時,求
時,求![]() 的度數和點
的度數和點![]() 的坐標;
的坐標;
(Ⅱ)連接![]() ,當
,當![]() 時,求
時,求![]() 的面積;
的面積;
(Ⅲ)當射線![]() 交線段
交線段![]() 于點
于點![]() 時,求
時,求![]() 的最大值.(直接寫出答案)
的最大值.(直接寫出答案)
在研究第(Ⅱ)問時,師生有如下對話:
師:我們可以嘗試通過加輔助線,構造出直角三角形,尋找方程的思路來解決問題.
小明:我是這樣想的,延長![]() 與
與![]() 軸交于
軸交于![]() 點,于是出現了
點,于是出現了![]() .
.
小雨:我和你想的不一樣,我過點![]() 作
作![]() 軸的平行線,出現了兩個
軸的平行線,出現了兩個![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b與反比例函數![]() 的圖象交于A(m,6),B(3,n)兩點.
的圖象交于A(m,6),B(3,n)兩點.
(1)求一次函數的解析式;
(2)根據圖象直接寫出![]() 的x的取值范圍;
的x的取值范圍;
(3)求△AOB的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
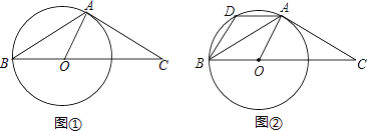
【題目】已知△ABC中,AB=AC,∠BAC=120°,在BC上取一點O,以O為圓心、OB為半徑作圓,且⊙O過A點.
(1)如圖①,若⊙O的半徑為5,求線段OC的長;
(2)如圖②,過點A作AD∥BC交⊙O于點D,連接BD,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是一座古拱橋的截面圖,拱橋橋洞的上沿是拋物線形狀,當水面的寬度為10m時,橋洞與水面
的最大距離是5m.
(1)經過討論,同學們得出三種建立平面直角坐標系的方案(如下圖)
你選擇的方案是_____(填方案一,方案二,或方案三),則B點坐標是______,求出你所選方案中的拋物線的表達式;
(2)因為上游水庫泄洪,水面寬度變為6m,求水面上漲的高度.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,矩形![]() 的頂點
的頂點![]() 在
在![]() 軸的正半軸上,
軸的正半軸上,![]() .對角線
.對角線![]() 相交于點
相交于點![]() ,反比例函數
,反比例函數![]() 的圖像經過點
的圖像經過點![]() ,分別與
,分別與![]() 交于點
交于點![]() .
.
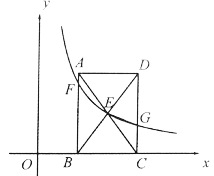
(1)若![]() ,求
,求![]() 的值;
的值;
(2)連接![]() ,若
,若![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知銳角△ABC中,AB=AC,邊BC長為6,高AD長為4,正方形PQMN的兩個頂點在△ABC一邊上,另兩個頂點分別在△ABC的另兩邊上,則正方形PQMN的邊長為( )
A.![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com