
【題目】在△ABC中,AC=6![]() ,點(diǎn)D為直線AB上一點(diǎn),且AB=3BD,直線CD與直線BC所夾銳角的正切值為
,點(diǎn)D為直線AB上一點(diǎn),且AB=3BD,直線CD與直線BC所夾銳角的正切值為![]() ,并且CD⊥AC,則BC的長(zhǎng)為________.
,并且CD⊥AC,則BC的長(zhǎng)為________.
【答案】![]() 或15
或15
【解析】
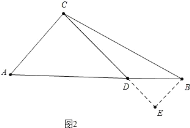
如圖1中,當(dāng)點(diǎn)D在AB的延長(zhǎng)線上時(shí),作BE⊥CD垂足為E,先求出BE,EC,在RT△BCE中利用勾股定理即可解決,如圖2中,當(dāng)點(diǎn)D在線段AB上時(shí),作BE⊥CD于E,方法類(lèi)似第一種情形.
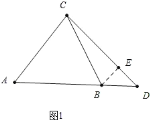
解:如圖1中,當(dāng)點(diǎn)D在AB的延長(zhǎng)線上時(shí),作BE⊥CD垂足為E,
∵AC⊥CD,
∴AC∥BE,
∴![]() ,
,
∵AC=![]() ,
,
∴BE=![]() ,
,
∵tan∠BCE=![]() ,
,
∴EC=2BE=![]() ,
,
∴BC=![]() .
.
如圖2中,當(dāng)點(diǎn)D在線段AB上時(shí),作BE⊥CD于E,
∵AC∥BE,AC=![]() ,
,
∴![]() ,
,
∴BE=![]() ,
,
∵tan∠BCE=![]() ,
,
∴EC=2BE=![]() ,
,
∴BC=![]()
故答案為:![]() 或15.
或15.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
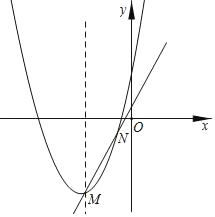
【題目】如圖,已知拋物線y=x2+px+q的對(duì)稱(chēng)軸為直線x=﹣2,過(guò)其頂點(diǎn)M的一條直線y=kx+b與該拋物線的另一個(gè)交點(diǎn)為N(﹣1,﹣1).若要在y軸上找一點(diǎn)P,使得PM+PN最小,則點(diǎn)P的坐標(biāo)為( ).
A. (0,﹣2) B. (0,﹣![]() ) C. (0,﹣
) C. (0,﹣![]() ) D. (0,﹣
) D. (0,﹣![]() )
)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋一枚均勻硬幣正面朝上的概率為![]() ,下列說(shuō)法錯(cuò)誤的是
,下列說(shuō)法錯(cuò)誤的是![]()
![]()
A. 連續(xù)拋一枚均勻硬幣2次必有1次正面朝上
B. 連續(xù)拋一枚均勻硬幣10次都可能正面朝上
C. 大量反復(fù)拋一枚均勻硬幣,平均每100次出現(xiàn)正面朝上50次
D. 通過(guò)拋一枚均勻硬幣確定誰(shuí)先發(fā)球的比賽規(guī)則是公平的
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,∠C=150°,AC=4,tanB=![]() .
.
(1)求BC的長(zhǎng);
(2)利用此圖形求tan15°的值(精確到0.1,參考數(shù)據(jù):![]() ≈1.4,
≈1.4,![]() ≈1.7,
≈1.7,![]() ≈2.2).
≈2.2).
![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,矩形![]() 中,點(diǎn)
中,點(diǎn)![]() 分別在邊
分別在邊![]() 與
與![]() 上,點(diǎn)
上,點(diǎn)![]() 在對(duì)角線
在對(duì)角線![]() 上,
上,![]() ,
,![]() .
.
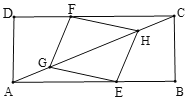
![]() 求證:四邊形
求證:四邊形![]() 是平行四邊形.
是平行四邊形.
![]() 若
若![]() ,
,![]() ,
,![]() ,求
,求![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
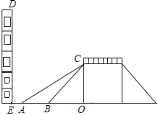
【題目】如圖是某一過(guò)街天橋的示意圖,天橋高![]() 為
為![]() 米,坡道傾斜角
米,坡道傾斜角![]() 為
為![]() ,在距
,在距![]() 點(diǎn)
點(diǎn)![]() 米處有一建筑物
米處有一建筑物![]() .為方便行人上下天橋,市政部門(mén)決定減少坡道的傾斜角,但要求建筑物與新坡角
.為方便行人上下天橋,市政部門(mén)決定減少坡道的傾斜角,但要求建筑物與新坡角![]() 處之間地面要留出不少于
處之間地面要留出不少于![]() 米寬的人行道.
米寬的人行道.
![]() 若將傾斜角改建為
若將傾斜角改建為![]() (即
(即![]() ),則建筑物
),則建筑物![]() 是否要拆除?(
是否要拆除?(![]() )
)
![]() 若不拆除建筑物
若不拆除建筑物![]() ,則傾斜角最小能改到多少度(精確到
,則傾斜角最小能改到多少度(精確到![]() )?
)?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在正方形![]() 中,邊長(zhǎng)為2的等邊三角形
中,邊長(zhǎng)為2的等邊三角形![]() 的頂點(diǎn)
的頂點(diǎn)![]() ,
,![]() 分別在
分別在![]() 和
和![]() 上,則正方形
上,則正方形![]() 的面積等于_________.
的面積等于_________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知拋物線y1=﹣x2+4x和直線y2=2x.我們規(guī)定:當(dāng)x取任意一個(gè)值時(shí),x對(duì)應(yīng)的函數(shù)值分別為y1和y2,若y1≠y2,取y1和y2中較小值為M;若y1=y2,記M=y1=y2.①當(dāng)x>2時(shí),M=y2;②當(dāng)x<0時(shí),M隨x的增大而增大;③使得M大于4的x的值不存在;④若M=2,則x=1.上述結(jié)論正確的是_____(填寫(xiě)所有正確結(jié)論的序號(hào)).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,AB=AC,以AB為直徑的圓交AC于點(diǎn)D,交BC于點(diǎn)E,延長(zhǎng)AE至點(diǎn)F,使EF=AE,連接FB,F(xiàn)C.
(1)求證:四邊形ABFC是菱形;
(2)若AD=7,BE=2,求半圓和菱形ABFC的面積.

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com