
【題目】2019年4月23日,是第23個世界讀書日.為了推進中華傳統文化教育,營造濃厚的讀書氛圍,我市某學校舉辦了“讓讀書成為習慣,讓書香溢病校園”主題活動.為了解學生每周閱讀時間,該校隨機抽取了部分學生進行調查,根據調查結果,將閱詼時間![]() (單位:小時)分成了
(單位:小時)分成了![]() 組,
組, ![]()
![]()
![]() ,下圖是根據這組數據繪制的兩幅不完整的統計圖.請你結合圖中所給信息解答下列問題:
,下圖是根據這組數據繪制的兩幅不完整的統計圖.請你結合圖中所給信息解答下列問題:
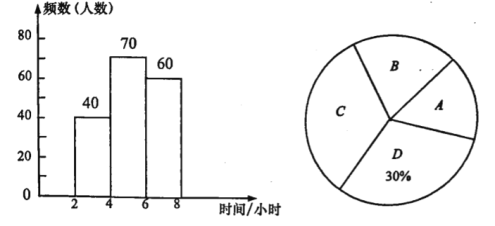
(1)這次隨機抽取了 名學生進行調查;
(2)補全頻數分布直方圖;
(3)計算扇形統計圖中扇形![]() 的圓心角的度數;
的圓心角的度數;
(4)若該校共有![]() 名學生,請你估計每周閱讀時間不足
名學生,請你估計每周閱讀時間不足![]() 小時的學生共有多少名?
小時的學生共有多少名?
【答案】(1) 200;(2)見詳解;(3) 72°;(4) 1050
【解析】
(1)D組的人數除以D組的百分比,即可求解;
(2)先求出A組的學生數,即可補全頻數分布直方圖;
(3)求出B組學生數占總數的百分比,再乘以360°,即可求解;
(4)先求出每周閱讀時間不足![]() 小時的學生占總數的百分比,再乘以3000,即可求解.
小時的學生占總數的百分比,再乘以3000,即可求解.
(1)60÷30%=200(名),
故答案是:200;
(2)A組學生有:200-40-70-60=30(名),
頻數分布直方圖如下:
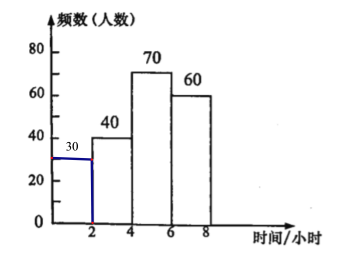
(3)40÷200=0.2,
360°×0.2=72°,
答:扇形![]() 的圓心角的度數為72°;
的圓心角的度數為72°;
(4)(30+40) ÷200=![]() ,
,
3000×![]() =1050(名),
=1050(名),
答:估計每周閱讀時間不足![]() 小時的學生共有1050名.
小時的學生共有1050名.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】在如圖的2016年6月份的日歷表中,任意框出表中豎列上三個相鄰的數,這三個數的和不可能是( )

A. 27 B. 51 C. 69 D. 72
查看答案和解析>>
科目:初中數學 來源: 題型:
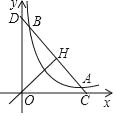
【題目】如圖,已知直線y=﹣x+b(b>0)與其垂線y=x交于H,與雙曲線c:y=![]() (k>0)在第一象限交于A,B,與兩坐標軸交于C,D.
(k>0)在第一象限交于A,B,與兩坐標軸交于C,D.
(1)當A的坐標為(2,1)時,求k的值和OH的長;
(2)若CH2﹣HA2=4,求雙曲線c的方程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A、B分別在x軸、y軸上.
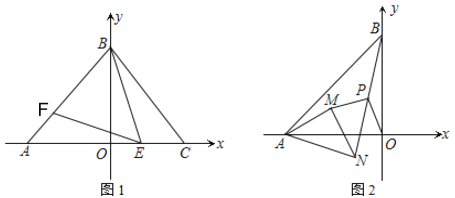
(1)如圖1,點A與點C關于y軸對稱,點E、F分別是線段AC、AB上的點(點E不與點A、C重合),且∠BEF=∠BAO.若∠BAO=2∠OBE,求證:AF=CE;
(2)如圖2,若OA=OB,在點A處有一等腰△AMN繞點A旋轉,且AM=MN,∠AMN=90°.連接BN,點P為BN的中點,試猜想OP和MP的數量關系和位置關系,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
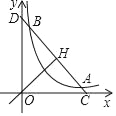
【題目】如圖,已知直線y=﹣x+b(b>0)與其垂線y=x交于H,與雙曲線c:y=![]() (k>0)在第一象限交于A,B,與兩坐標軸交于C,D.
(k>0)在第一象限交于A,B,與兩坐標軸交于C,D.
(1)當A的坐標為(2,1)時,求k的值和OH的長;
(2)若CH2﹣HA2=4,求雙曲線c的方程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某次試驗中,測得兩個變量v和m的對應數據如下表,則v和m之間的關系最接近下列函數中的( )
m | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
v | ﹣6.10 | ﹣2.90 | ﹣2.01 | ﹣1.51 | ﹣1.19 | ﹣1.05 | ﹣0.86 |
A. v=m2﹣2 B. v=﹣6m C. v=﹣3m﹣1 D. v=![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某服裝店準備購進甲、乙兩種服裝出售,甲種每件售價120元,乙種每件售價90元.每件甲服裝的進價比乙服裝的進價貴20元,購進3件甲服裝的費用和購進4件乙服裝的費用相等,現計劃購進兩種服裝共100件,其中甲種服裝不少于65件.
(1)甲種服裝進價為 元/件,乙種服裝進價為 元/件;
(2)若購進這100件服裝的費用不得超過7500元.
①求甲種服裝最多購進多少件?
②該服裝店對甲種服裝每件降價![]() 元,乙種服裝價格不變,如果這100件服裝都可售完,那么該服裝店如何進貨才能獲得最大利潤?
元,乙種服裝價格不變,如果這100件服裝都可售完,那么該服裝店如何進貨才能獲得最大利潤?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小軍自制的勻速直線運動遙控車模型甲、乙兩車同時分別從![]() 、
、![]() 出發,沿直線軌道同時到達
出發,沿直線軌道同時到達![]() 處,已知乙的速度是甲的速度的1.5倍,甲、乙兩遙控車與
處,已知乙的速度是甲的速度的1.5倍,甲、乙兩遙控車與![]() 處的距離
處的距離![]() 、
、![]() (米)與時間
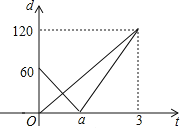
(米)與時間![]() (分鐘)的函數關系如圖所示,則下列結論中:①
(分鐘)的函數關系如圖所示,則下列結論中:①![]() 的距離為120米;②乙的速度為60米/分;③
的距離為120米;②乙的速度為60米/分;③![]() 的值為
的值為![]() ;④若甲、乙兩遙控車的距離不少于10米時,兩車信號不會產生互相干擾,則兩車信號不會產生互相干擾的
;④若甲、乙兩遙控車的距離不少于10米時,兩車信號不會產生互相干擾,則兩車信號不會產生互相干擾的![]() 的取值范圍是
的取值范圍是![]() ,其中正確的有( )個
,其中正確的有( )個
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB=AC,AE=AF,BE與CF交于點D,則對于下列結論:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分線上.其中正確的是( )
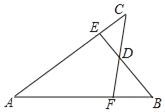
A. ① B. ② C. ①和② D. ①②③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com