
【題目】在平面直角坐標(biāo)系中,直線![]() 與x軸交于點B,與y軸交于點C,二次函數(shù)
與x軸交于點B,與y軸交于點C,二次函數(shù)![]() 的圖象經(jīng)過點B,C兩點,且與x軸的負(fù)半軸交于點A,動點D在直線BC下方的二次函數(shù)圖象上.
的圖象經(jīng)過點B,C兩點,且與x軸的負(fù)半軸交于點A,動點D在直線BC下方的二次函數(shù)圖象上.
(1)求二次函數(shù)的表達式;
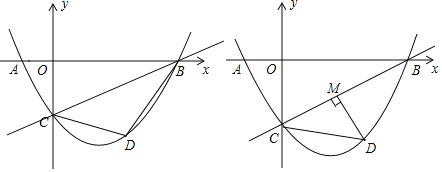
(2)如圖1,連接DC,DB,設(shè)△BCD的面積為S,求S的最大值;
(3)如圖2,過點D作DM⊥BC于點M,是否存在點D,使得△CDM中的某個角恰好等于∠ABC的2倍?若存在,直接寫出點D的橫坐標(biāo);若不存在,請說明理由.
【答案】(1)二次函數(shù)的表達式為:![]() ;(2)4;(3)
;(2)4;(3)![]() 或
或![]() .
.
【解析】
(1)先求得點B、C的坐標(biāo),再代入![]() 求得b、c的值,即可得二次函數(shù)的表達式;(2)過點
求得b、c的值,即可得二次函數(shù)的表達式;(2)過點![]() 作
作![]() 軸于點
軸于點![]() ,交
,交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,設(shè)
,設(shè)![]() ,則
,則![]() .用含有a的代數(shù)式表示出
.用含有a的代數(shù)式表示出![]() 的長,再根據(jù)
的長,再根據(jù)![]() 得到S與a的二次函數(shù)關(guān)系,利用二次函數(shù)的性質(zhì)即可解答;(3)在x軸上取點K,使CK=BK,則∠OKC=2∠ABC,過點B作BQ∥MD交CD延長線于點Q,過點Q作QH⊥x軸于點H,分∠DCM=∠QCB=2∠ABC和∠CDM=∠CQB=2∠ABC兩種情況求點D的橫坐標(biāo)即可.
得到S與a的二次函數(shù)關(guān)系,利用二次函數(shù)的性質(zhì)即可解答;(3)在x軸上取點K,使CK=BK,則∠OKC=2∠ABC,過點B作BQ∥MD交CD延長線于點Q,過點Q作QH⊥x軸于點H,分∠DCM=∠QCB=2∠ABC和∠CDM=∠CQB=2∠ABC兩種情況求點D的橫坐標(biāo)即可.
(1)直線![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() ;當(dāng)
;當(dāng)![]() 時,
時,![]() ,
,
∴![]() ,
,![]() .
.
∵二次函數(shù)![]() 的圖象經(jīng)過
的圖象經(jīng)過![]() ,
,![]() 兩點,
兩點,
∴ 解得
解得
∴二次函數(shù)的表達式為:![]() .
.
(2)過點![]() 作
作![]() 軸于點
軸于點![]() ,交
,交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,
,

依題意設(shè)![]() ,則
,則![]() .
.
其中![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
∵![]() ,∴拋物線開口向下.
,∴拋物線開口向下.
又∵![]() ,
,
∴當(dāng)![]() 時,
時,![]() 有最大值,
有最大值,![]() ;
;
(3)![]() 或
或![]()
在![]() 軸上取點
軸上取點![]() ,使
,使![]() ,則
,則![]() .
.
過點![]() 作
作![]() ∥
∥![]() 交
交![]() 延長線于點
延長線于點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,
,

設(shè)點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,則
,則![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,解得
,解得![]() .∴
.∴![]() .
.
當(dāng)![]() 時,
時,
∴![]() .
.
∴![]() .
.
易證![]() ∽
∽![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,
∴直線![]() 的函數(shù)表達式為:
的函數(shù)表達式為:![]() .
.
由![]() ,解得:
,解得:![]() ,
,![]() (舍).
(舍).
∴![]() 點的橫坐標(biāo)為2.
點的橫坐標(biāo)為2.
②當(dāng)![]() 時,方法同①,可確定點
時,方法同①,可確定點![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() .
.


 陽光課堂課時優(yōu)化作業(yè)系列答案
陽光課堂課時優(yōu)化作業(yè)系列答案科目:初中數(shù)學(xué) 來源: 題型:
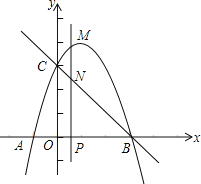
【題目】如圖,拋物線y=﹣x2+bx+c與x軸交于A(﹣1,0),B兩點(點A在點B的左側(cè)),與y軸交于點C(0,3),作直線BC.動點P在x軸上運動,過點P作PM⊥x軸,交拋物線于點M,交直線BC于點N,設(shè)點P的橫坐標(biāo)為m.
(1)求拋物線的解析式;
(2)當(dāng)點P在線段OB上運動時,求線段MN的最大值;
(3)是否存在點P,使得以點C、O、M、N為頂點的四邊形是平行四邊形?若存在,請直接寫出m的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
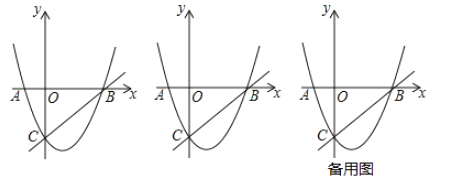
【題目】如圖,拋物線![]() 經(jīng)過
經(jīng)過![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() .
.
(1)求此拋物線的解析式;
(2)已知點![]() 為
為![]() 軸上一點,點
軸上一點,點![]() 關(guān)于直線
關(guān)于直線![]() 的對稱點為
的對稱點為![]() .
.
①當(dāng)點![]() 剛好落在第四象限的拋物線上時,求出點
剛好落在第四象限的拋物線上時,求出點![]() 的坐標(biāo);
的坐標(biāo);
②點![]() 在拋物線上,連接
在拋物線上,連接![]() ,是否存在點
,是否存在點![]() ,使
,使![]() 為等腰直角三角形?若存在,請直接寫出
為等腰直角三角形?若存在,請直接寫出![]() 點的坐標(biāo);若不存在,請說明理由.
點的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
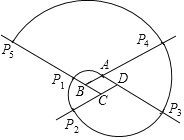
【題目】如圖,四邊形ABCD是邊長為1的菱形,∠ABC=60°.動點P第1次從點A處開始,沿以B為圓心,AB為半徑的圓弧運動到CB延長線,記為點P1;第2次從點P1開始,沿以C為圓心,CP1為半徑的圓弧運動到DC的延長線,記為點P2;第3次從P2開始,沿以D為圓心,DP2為半徑的圓弧運動到AD的延長線,記為點P3;第4次從點P3開始,沿以A為圓心,AP3為半徑的圓弧運動到BA的延長線,記為點P4;…..如此運動下去,當(dāng)點P運動到P20時,點P所運動的路程為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在矩形ABCD中,AB=8,點H是直線AB邊上的一個點,連接DH交直線CB的干點E,交直線AC于點F,連接BF.
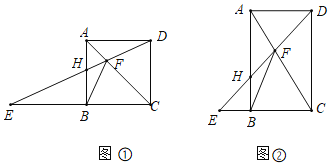
(1)如圖①,點H在AB邊上,若四邊形ABCD是正方形,求證:△ADF≌△ABF;
(2)在(1)的條件下,若△BHF為等腰三角形,求HF的長;
(3)如圖②,若tan∠ADH=![]() ,是否存在點H,使得△BHF為等腰三角形?若存在,求該三角形的腰長;若不存在,試說明理由.
,是否存在點H,使得△BHF為等腰三角形?若存在,求該三角形的腰長;若不存在,試說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四邊形ABCD中,AD=BC,∠A=∠B,E為AB的中點,連結(jié)CE,DE.
(1)求證:△ADE≌△BCE.
(2)若∠A=70°,∠BCE=60°,求∠CDE的度數(shù).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
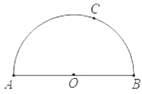
【題目】如圖,![]() 為半圓
為半圓![]() 的直徑,點
的直徑,點![]() 為半圓上任一點.
為半圓上任一點.
(1)若![]() ,過點
,過點![]() 作半圓
作半圓![]() 的切線交直線
的切線交直線![]() 于點
于點![]() .求證:
.求證:![]() ;
;
(2)若![]() ,過點
,過點![]() 作
作![]() 的平行線交半圓
的平行線交半圓![]() 于點
于點![]() .當(dāng)以點
.當(dāng)以點![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形為菱形時,求
為頂點的四邊形為菱形時,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為積極響應(yīng)市委政府“加快建設(shè)天藍水碧地綠的美麗長沙”的號召,我市某街道決定從備選的五種樹中選購一種進行栽種.為了更好地了解社情民意,工作人員在街道轄區(qū)范圍內(nèi)隨機抽取了部分居民,進行“我最喜歡的一種樹”的調(diào)查活動(每人限選其中一種樹),并將調(diào)查結(jié)果整理后,繪制成如圖兩個不完整的統(tǒng)計圖:

請根據(jù)所給信息解答以下問題:
(1)這次參與調(diào)查的居民人數(shù)為: ;
(2)請將條形統(tǒng)計圖補充完整;
(3)請計算扇形統(tǒng)計圖中“楓樹”所在扇形的圓心角度數(shù);
(4)已知該街道轄區(qū)內(nèi)現(xiàn)有居民8萬人,請你估計這8萬人中最喜歡玉蘭樹的有多少人?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在Rt△ABC中,∠ACB=90°,AC=3,BC=4.點O為邊AB上一點(不與A重合)⊙O是以點O為圓心,AO為半徑的圓.當(dāng)⊙O與三角形邊的交點個數(shù)為3時,則OA的范圍( )
A.0<OA≤![]() 或2.5≤OA<5B.0<OA
或2.5≤OA<5B.0<OA![]() 或OA=2.5
或OA=2.5
C.OA=2.5D.OA=2.5或![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com