
【題目】已知拋物線![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 和
和![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左邊),點
的左邊),點![]() 為拋物線的頂點.
為拋物線的頂點.
(1)求拋物線的函數(shù)解析式;
(2)畫出此二次函數(shù)的大致圖像;
(3)點![]() 為線段
為線段![]() 上一點(點
上一點(點![]() 不與點
不與點![]() 、
、![]() 重合),過點
重合),過點![]() 作
作![]() 軸的垂線,與拋物線交于點
軸的垂線,與拋物線交于點![]() ,過點
,過點![]() 作
作![]() 交拋物線于點
交拋物線于點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() .若點
.若點![]() 在點
在點![]() 左邊,求當(dāng)矩形
左邊,求當(dāng)矩形![]() 的周長最大時點
的周長最大時點![]() 的橫坐標(biāo).
的橫坐標(biāo).
【答案】(1)![]() ;(2)見解析;(3)-2
;(2)見解析;(3)-2
【解析】
(1)把A,B兩點坐標(biāo)分別代入解析式即可求解;
(2)求出對稱軸,與坐標(biāo)軸的交點可畫出大致圖像;
(3)設(shè)點M的橫坐標(biāo)為m,則PM和MN的長度可以用m表示,從而得出矩形的周長與m的函數(shù)關(guān)系式,最后利用二次函數(shù)的性質(zhì)求解.
解:(1)把![]() 、
、![]() 兩點坐標(biāo)分別代入
兩點坐標(biāo)分別代入![]()
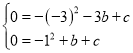
解得![]() ,
,![]() ,
,
∴![]()
(2)函數(shù)與![]() 軸的交點為
軸的交點為![]() ;與
;與![]() 軸的交點坐標(biāo)
軸的交點坐標(biāo)![]() ;頂點坐標(biāo)
;頂點坐標(biāo)![]() ;函數(shù)圖像如圖所示:
;函數(shù)圖像如圖所示:
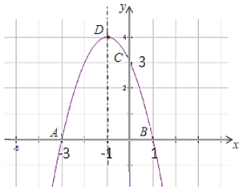
(3)由拋物線![]() 可知,對稱軸為直線
可知,對稱軸為直線![]() ,
,
設(shè)![]() 點的橫坐標(biāo)為
點的橫坐標(biāo)為![]()
![]() ,則
,則![]() ,
,![]() ,
,
∴矩形![]() 的周長
的周長![]() ,
,
∴當(dāng)![]() 時矩形的周長最大.即
時矩形的周長最大.即![]() 的橫坐標(biāo)為-2.
的橫坐標(biāo)為-2.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形OABC的一個頂點O是平面直角坐標(biāo)系的原點,頂點A,C分別在y軸和x軸上,P為邊OC上的一個動點,且PQ⊥BP,PQ=BP,當(dāng)點P從點C運動到點O時,可知點Q始終在某函數(shù)圖象上運動,則其函數(shù)圖象是( )
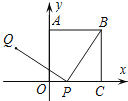
A.線段B.圓弧
C.雙曲線的一部分D.拋物線的一部分
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了解某市初中學(xué)生課外閱讀情況,調(diào)查小組對該市這學(xué)期初中學(xué)生閱讀課外書籍的冊數(shù)進行了抽樣調(diào)查,并根據(jù)調(diào)查結(jié)果繪制成如下統(tǒng)計圖.
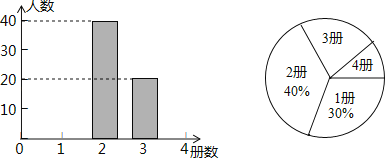
根據(jù)統(tǒng)計圖提供的信息,解答下列問題:
(1)本次抽樣調(diào)查的樣本容量是 ;
(2)補全條形統(tǒng)計圖;
(3)該市共有12000名初中生,估計該市初中學(xué)生這學(xué)期課外閱讀超過2冊的人數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】知,拋物線![]() (a
(a![]() 0)的頂點為A(s,t)(其中s
0)的頂點為A(s,t)(其中s![]() 0) .
0) .
(1)若拋物線經(jīng)過(2,2)和(-3,37)兩點,且s=3.
①求拋物線的解析式;
②若n>3, 設(shè)點M(![]() ),N(
),N(![]() )在拋物線上,比較
)在拋物線上,比較![]() ,
,![]() 的大小關(guān)系,并說明理由;
的大小關(guān)系,并說明理由;
(2)若a=2,c=-2,直線![]() 與拋物線
與拋物線![]() 的交于點P和點Q,點P的橫坐標(biāo)為h,點Q的橫坐標(biāo)為h+3,求出b和h的函數(shù)關(guān)系式;
的交于點P和點Q,點P的橫坐標(biāo)為h,點Q的橫坐標(biāo)為h+3,求出b和h的函數(shù)關(guān)系式;
(3)若點A在拋物線![]() 上,且2≤s<3時,求a的取值范圍.
上,且2≤s<3時,求a的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知梯形ABCD中,AD∥BC,AB=AC,E是邊BC上的點,且∠AED=∠CAD,DE交AC于點F.
(1)求證:△ABE∽△DAF;
(2)當(dāng)ACFC=AEEC時,求證:AD=BE.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩人要某風(fēng)景區(qū)游玩,每天某一時段開往該景區(qū)有三輛汽車(票價相同),但是他們不清楚這三輛車的舒適程度,也不知道汽車開來的順序,兩人采用了不同的乘車方案:
甲無論如何總是上開來的第一輛車,而乙則是先觀察后上車,當(dāng)?shù)谝惠v車開來時,他不上車,而是仔細(xì)觀察車輛的舒適狀況,如果第二輛車狀況比第一輛好,他就上第二輛車,如果第二輛不比第一輛好,他就上第三輛車.這三輛車的舒適程度為上、中、下三等,請解決下面的問題:
(1)請用畫樹形圖或列表的方法分析這三輛車出現(xiàn)的先后順序,寫出所有可能的結(jié)果;(用上中下表示)
(2)分析甲、乙兩人采用的方案,誰的方案使自己坐上上等車的可能性大,說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
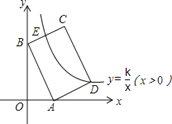
【題目】如圖,在平面直角坐標(biāo)系中,矩形ABCD的邊AB:BC=3:2,點A(3,0),B(0,6)分別在x軸,y軸上,反比例函數(shù)y=![]() (x>0)的圖象經(jīng)過點D,且與邊BC交于點E,則點E的坐標(biāo)為__.
(x>0)的圖象經(jīng)過點D,且與邊BC交于點E,則點E的坐標(biāo)為__.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
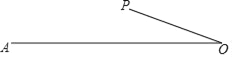
【題目】如圖,線段OA=2,OP=1,將線段OP繞點O任意旋轉(zhuǎn)時,線段AP的長度也隨之改變,則下列結(jié)論:
①AP的最小值是1,最大值是4;
②當(dāng)AP=2時,△APO是等腰三角形;
③當(dāng)AP=1時,△APO是等腰三角形;
④當(dāng)AP=![]() 時,△APO是直角三角形;
時,△APO是直角三角形;
⑤當(dāng)AP=![]() 時,△APO是直角三角形.
時,△APO是直角三角形.
其中正確的是( )
A. ①④⑤ B. ②③⑤ C. ②④⑤ D. ③④⑤
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
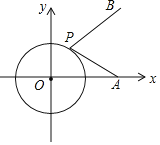
【題目】如圖,在平面直角坐標(biāo)系中,點A(4,0),B(4,4),點P在半徑為2的圓O上運動,則![]() 的最小值為____________.
的最小值為____________.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com