
【題目】如圖1,在△ABC中,∠ACB=90°,BC=2,∠A=30°,點E,F分別是線段BC,AC的中點,連結EF.
(1)線段BE與AF的位置關系是 ,![]() = .
= .
(2)如圖2,當△CEF繞點C順時針旋轉a時(0°<a<180°),連結AF,BE,(1)中的結論是否仍然成立.如果成立,請證明;如果不成立,請說明理由.
(3)如圖3,當△CEF繞點C順時針旋轉a時(0°<a<180°),延長FC交AB于點D,如果AD=6﹣2![]() ,求旋轉角a的度數.
,求旋轉角a的度數.
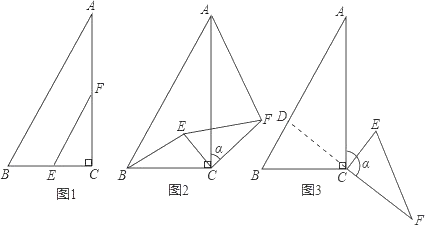
【答案】(1)互相垂直;![]() (2)結論仍然成立(3)135°
(2)結論仍然成立(3)135°
【解析】
試題(1)結合已知角度以及利用銳角三角函數關系求出AB的長,進而得出答案;
(2)利用已知得出△BEC∽△AFC,進而得出∠1=∠2,即可得出答案;
(3)過點D作DH⊥BC于H,則DB=4-(6-2![]() )=2
)=2![]() -2,進而得出BH=
-2,進而得出BH=![]() -1,DH=3-
-1,DH=3-![]() ,求出CH=BH,得出∠DCA=45°,進而得出答案.
,求出CH=BH,得出∠DCA=45°,進而得出答案.
試題解析:(1)如圖1,線段BE與AF的位置關系是互相垂直;
∵∠ACB=90°,BC=2,∠A=30°,
∴AC=2![]() ,
,
∵點E,F分別是線段BC,AC的中點,
∴![]() =
=![]()
(2))如圖2,∵點E,F分別是線段BC,AC的中點,

∴EC=![]() BC,FC=
BC,FC=![]() AC,
AC,
∴![]() ,
,
∵∠BCE=∠ACF=α,
∴△BEC∽△AFC,
∴![]() ,
,
∴∠1=∠2,
延長BE交AC于點O,交AF于點M
∵∠BOC=∠AOM,∠1=∠2
∴∠BCO=∠AMO=90°
∴BE⊥AF;
(3)如圖3,

∵∠ACB=90°,BC=2,∠A=30°∴AB=4,∠B=60°
過點D作DH⊥BC于H∴DB=4-(6-2![]() )=2
)=2![]() -2,
-2,
∴BH=![]() -1,DH=3-
-1,DH=3-![]() ,又∵CH=2-(
,又∵CH=2-(![]() -1)=3-
-1)=3-![]() ,
,
∴CH=BH,∴∠HCD=45°,∴∠DCA=45°,α=180°-45°=135°.


科目:初中數學 來源: 題型:
【題目】某超市銷售一種商品,每件的成本每千克18元,規定每千克售價不低于成本,且獲利不得高于100%,經市場調查,每天的銷售量y(千克)與每千克售價x(元)滿足一次函數關系,部分數據如下表:
售價x(元/千克) | 40 | 39 | 38 | 37 |
銷售量y(千克) | 20 | 22 | 24 | 26 |
(1)求y與x之間的函數表達式;
(2)設商品每天的總利潤為W(元),求W與x之間的函數表達式(利潤=收入﹣成本),并指出售價為多少元時獲得最大利潤,最大利潤是多少?
(3)該超市若想每天銷售利潤不低于480元,請結合函數圖象幫助超市確定產品的銷售單價范圍?
查看答案和解析>>
科目:初中數學 來源: 題型:
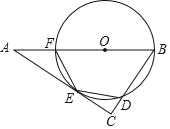
【題目】如圖,點O是△ABC的邊AB上一點,⊙O與邊AC相切于點E,與邊BC,AB分別相交于點D,F,且DE=EF.
(1)求證:∠C=90°;
(2)當BC=3,sinA=![]() 時,求AF的長.
時,求AF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=x2+bx+c的圖象交于點(4,﹣3),(﹣1,12).
(1)求二次函數的解析式;
(2)二次函數與x軸交于點A,B,與y軸交于點C,求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)填空:如圖,我們知道,一條線段OA繞著它的一個端點O旋轉一周,另一個端點所形成的圖形叫做 ;一個矩形ABCD繞著它的邊AB旋轉一周所形成的圖形叫做 ;
(2)如圖,將一個直角三角形ABC(∠C=900)繞著它的直角邊AC旋轉一周,也能形成一個幾何圖形。
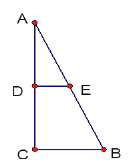
(a)在圖中畫出這個旋轉圖形的草圖,并說出它的名稱。
(b)如果ΔABC中AC=20,BC=15,把這個旋轉圖形沿著ΔABC的中位線DE且垂直于AC的方向橫截,得到一個什么樣的圖形?并請你計算所截圖形的上半部分的全面積。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,已知AB=3,AD=8,點E為BC的中點,連接AE,EF是∠AEC的平分線,交AD于點F,則FD=( )

A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中數學 來源: 題型:
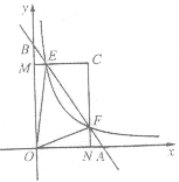
【題目】如圖,在平面直角坐標系xOy中,直線AB與x軸、y軸分別交于點A,B,與反比例函數![]() (
(![]() 為常數,且
為常數,且![]() )在第一象限的圖象交于點E,F.過點E作EM⊥y軸于M,過點F作FN⊥x軸于N,直線EM與FN交于點C.若
)在第一象限的圖象交于點E,F.過點E作EM⊥y軸于M,過點F作FN⊥x軸于N,直線EM與FN交于點C.若![]() (
(![]() 為大于l的常數).記△CEF的面積為
為大于l的常數).記△CEF的面積為![]() ,△OEF的面積為
,△OEF的面積為![]() ,則
,則![]() =________. (用含
=________. (用含![]() 的代數式表示)
的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
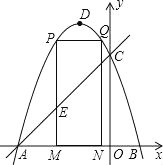
【題目】如圖,拋物線y=﹣x2﹣2x+3的圖象與x軸交于A、B兩點(點A在點B的左邊),與y軸交于點C,點D為拋物線的頂點.
(1)求點A、B、C的坐標;
(2)點M(m,0)為線段AB上一點(點M不與點A、B重合),過點M作x軸的垂線,與直線AC交于點E,與拋物線交于點P,過點P作PQ∥AB交拋物線于點Q,過點Q作QN⊥x軸于點N,可得矩形PQNM.如圖,點P在點Q左邊,試用含m的式子表示矩形PQNM的周長;
(3)當矩形PQNM的周長最大時,m的值是多少?并求出此時的△AEM的面積;
(4)在(3)的條件下,當矩形PMNQ的周長最大時,連接DQ,過拋物線上一點F作y軸的平行線,與直線AC交于點G(點G在點F的上方).若FG=2![]() DQ,求點F的坐標.
DQ,求點F的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com