
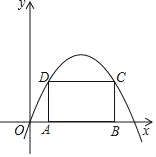
【題目】如圖,A,B兩點在x軸的正半軸上運動,四邊形ABCD是矩形,C,D兩點在拋物線y=﹣x2+8x上.
(1)若OA=1,求矩形ABCD的周長;
(2)設(shè)OA=m(0<m<4),求出四邊形ABCD的周長L關(guān)于m的函數(shù)表達(dá)式;
(3)在(2)的條件下求L的最大值.
【答案】(1)26;(2)L=﹣2m2+12m+16,(3)34.
【解析】(1)根據(jù)自變量與函數(shù)值的對應(yīng)關(guān)系,可得D點坐標(biāo),根據(jù)矩形的周長公式,可得答案
(2)求L與m的函數(shù)解析式就是把m當(dāng)作已知量,求L,先求AD,它的長就是D點的縱坐標(biāo),再把D點縱坐標(biāo)代入函數(shù)解析式求C點橫坐標(biāo),C點橫坐標(biāo)與D點橫坐標(biāo)的差就是線段CD的長,用L=2(AD+CD),建立函數(shù)關(guān)系式.
(3)根據(jù)二次函數(shù)的性質(zhì),可得答案.
(1)當(dāng)x=1時,y=-1+8=7,即AD=7,D點坐標(biāo)為(1,7).
當(dāng)y=7時,-x2+8x=7,
解得x1=1,x2=7,
即AB=7-1=6,
矩形ABCD的周長=2(AD+AB)=2(7+6)=26;
(2)把x=m代入拋物線y=-x2+8x中,得AD=-m2+8m
把y=-m2+8m代入拋物線y=-m2+8m中,得
-m2+8m=-x2+8x
解得x1=m,x2=8-m
∴C的橫坐標(biāo)是8-m,故AB=8-m-m=8-2m
∴矩形的周長是L=2(-m2+8m)+2(8-2m)
即L=-2m2+12m+16.
(3)L=-2m2+12m+16化為頂點式,得
L=-2(m-3)2+34 (0<m<4),
當(dāng)m=3時,L最大=34,
在(2)的條件下求L的最大值是34.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,OB是∠AOC的平分線,OD是∠COE的平分線.
(1)若∠AOB=50°,∠DOE=35°,求∠BOD的度數(shù);
(2)若∠AOE=160°,∠COD=40°,求∠AOB的度數(shù).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
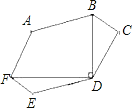
【題目】如圖所示,六邊ABCDEF中,AB平行且等于ED,AF平行且等于CD,BC平行且等于FE,對角線FD⊥BD.已知FD=24![]() ,BD=18
,BD=18![]() .則六邊形ABCDEF的面積是______.
.則六邊形ABCDEF的面積是______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知![]() 的三個頂點的坐標(biāo)分別為
的三個頂點的坐標(biāo)分別為![]() 、
、![]() 、
、![]() .
.
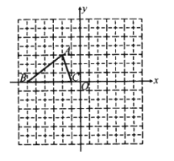
(1)請直接寫出點![]() 關(guān)于原點對稱的點的坐標(biāo);
關(guān)于原點對稱的點的坐標(biāo);
(2)將![]() 繞坐標(biāo)原點
繞坐標(biāo)原點![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() 得到
得到![]() ,畫出
,畫出![]() ,直接寫出點
,直接寫出點![]() 、
、![]() 的對應(yīng)點的點
的對應(yīng)點的點![]() 、
、![]() 坐標(biāo);
坐標(biāo);
(3)請直接寫出:以![]() 、
、![]() 、
、![]() 為頂點的平行四邊形的第四個頂點
為頂點的平行四邊形的第四個頂點![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
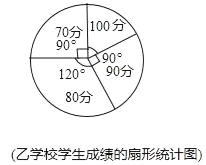
【題目】在“學(xué)科能力”展示活動中,某縣教育局決定在甲、乙兩校舉行“學(xué)科能力”比賽活動,規(guī)定甲、乙兩學(xué)校選派相同人數(shù)的選手參加,比賽結(jié)束后,發(fā)現(xiàn)參賽選手的成績是70分、80分、90分、l00分這四種成績中的一種,已知甲、乙兩校的選手獲得100分的人數(shù)相等.現(xiàn)根據(jù)甲、乙兩校選手的成績,繪制成兩幅不完整統(tǒng)計圖如下:
(1)請補(bǔ)全條形統(tǒng)計圖;
(2)比賽結(jié)束后,教育局決定對甲、乙兩校獲得100分的選手進(jìn)行集中培訓(xùn),培訓(xùn)后,從中隨機(jī)選取兩位選手參加市里的決賽,請用列表法或畫樹狀圖的方法,求所選兩位選手來自同一學(xué)校的概率.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】數(shù)軸上有![]() 、
、![]() 、
、![]() 三個點對應(yīng)的數(shù)分別是-22、-10、10.動點
三個點對應(yīng)的數(shù)分別是-22、-10、10.動點![]() 從
從 ![]() 出發(fā),以每秒3個單位的速度向點
出發(fā),以每秒3個單位的速度向點![]() 方向移動,設(shè)移動時間為
方向移動,設(shè)移動時間為![]() 秒,點Q以每秒1個單位的速度向右運動,
秒,點Q以每秒1個單位的速度向右運動, ![]() 點到達(dá)
點到達(dá)![]() 點后,再立即按原速返回點
點后,再立即按原速返回點![]() .
.
![]()
(1)點![]() 到達(dá)點
到達(dá)點![]() 時
時![]() 秒,點
秒,點![]() 向右運動的過程所表示的數(shù)為 ,點
向右運動的過程所表示的數(shù)為 ,點![]() 返回的過程中所表示的數(shù)為 ;
返回的過程中所表示的數(shù)為 ;
(2)當(dāng)![]() 為何值時,
為何值時, ![]() 、
、![]() 兩點之間的距離為4.
兩點之間的距離為4.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,矩形ABCD中,E是AD的中點,延長CE,BA交于點F,連接AC,DF.
(1)求證:四邊形ACDF是平行四邊形;
(2)當(dāng)CF平分∠BCD時,寫出BC與CD的數(shù)量關(guān)系,并說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,Rt△ABC中,∠ACB=90°,BC=5,AC=12,I是Rt△ABC的內(nèi)心,連接CI,AI,則△CIA外接圓的半徑為()
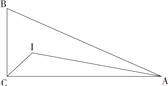
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1是邊長為![]() 的正方形薄鐵片,小明將其四角各剪去一個相同的小正方形(圖中陰影部分)后,發(fā)現(xiàn)剩余的部分能折成一個無蓋的長方體盒子,圖2為盒子的示意圖(鐵片的厚度忽略不計).
的正方形薄鐵片,小明將其四角各剪去一個相同的小正方形(圖中陰影部分)后,發(fā)現(xiàn)剩余的部分能折成一個無蓋的長方體盒子,圖2為盒子的示意圖(鐵片的厚度忽略不計).
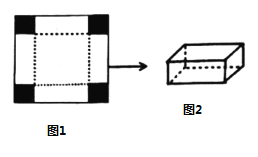
(1)設(shè)剪去的小正方形的邊長為![]() ,折成的長方體盒子的容積為
,折成的長方體盒子的容積為![]() ,直接寫出用只含字母
,直接寫出用只含字母![]() 的式子表示這個盒子的高為______
的式子表示這個盒子的高為______![]() ,底面積為______
,底面積為______![]() ,盒子的容積
,盒子的容積![]() 為______
為______![]() ,
,
(2)為探究盒子的體積與剪去的小正方形的邊長![]() 之間的關(guān)系,小明列表
之間的關(guān)系,小明列表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 324 |
| 588 | 576 | 500 |
| 252 | 128 |
填空:①![]() ______,
______,![]() ______;
______;
②由表格中的數(shù)據(jù)觀察可知當(dāng)![]() 的值逐漸增大時,
的值逐漸增大時,![]() 的值______.(從“逐漸增大”,“逐漸減小”“先增大后減小”,“先減小后增大”中選一個進(jìn)行填空)
的值______.(從“逐漸增大”,“逐漸減小”“先增大后減小”,“先減小后增大”中選一個進(jìn)行填空)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com