
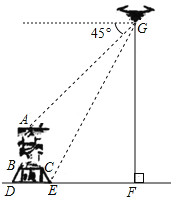
【題目】為了測量重慶有名的觀景點南山大金鷹的大致高度,小南同學使用的無人機進行觀察,當無人機與大金鷹側面在同一平面,且距離水平面垂直高度GF為100米時,小南調整攝像頭方向,當俯角為45°時,恰好可以拍攝到金鷹的頭頂A點;當俯角為63°時,恰好可以拍攝到金鷹底座點E.已知大金鷹是雄踞在一人造石臺上,石臺側面CE長12.5米,坡度為1:0.75,石臺上方BC長10米,頭部A點位于BC中點正上方.則金鷹自身高度約( )米.(結果保留一位小數,sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
作AM⊥DF于M,AHGF于H,則AM=HF,AH=MF,在Rt△EFG中,由三角函數求出EF=![]() ≈51.02,由石臺側面CE坡度為1:0.75,求出石臺側面CE寬度為12.5×
≈51.02,由石臺側面CE坡度為1:0.75,求出石臺側面CE寬度為12.5×![]() =7.5,高度為10,求出ME=
=7.5,高度為10,求出ME=![]() BC=12.5,得出AH=MF=63.52,證出△AGH是等腰直角三角形,得出GH=AH=63.52,求出AM=HF=100-63.52≈36.5(米),即可得出答案.
BC=12.5,得出AH=MF=63.52,證出△AGH是等腰直角三角形,得出GH=AH=63.52,求出AM=HF=100-63.52≈36.5(米),即可得出答案.
解:作AM⊥DF于M,AH⊥GF于H,如圖所示:
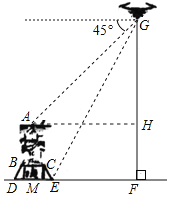
則AM=HF,AH=MF,
在Rt△EFG中,∠GEF=63°,
∵tan∠GEF=![]() ,∴EF=
,∴EF=![]() ≈
≈![]() =51.02,
=51.02,
∵石臺側面CE長12.5米,坡度為1:0.75,
∴石臺側面CE寬度為12.5×![]() =7.5,高度為12.5×
=7.5,高度為12.5×![]() =10,
=10,
∵石臺上方BC長10米,頭部A點位于BC中點正上方,
∴ME=![]() BC+7.5=5+7.5=12.5,
BC+7.5=5+7.5=12.5,
∴AH=MF=12.5+51.02=63.52,
在Rt△AGH中,∠AGH=90°-45°=45°,
∴△AGH是等腰直角三角形,
∴GH=AH=63.52,
∴AM=HF=100-63.52≈36.5(米),
∴金鷹自身高度約為36.5-10=26.5(米);
故選:A.


科目:初中數學 來源: 題型:
【題目】矩形![]() ,
,![]() ,
,![]() ,
,![]() ,(
,(![]() ),以
),以![]() 為旋轉中心順時針旋轉矩形
為旋轉中心順時針旋轉矩形![]() ,得到矩形
,得到矩形![]() .
.
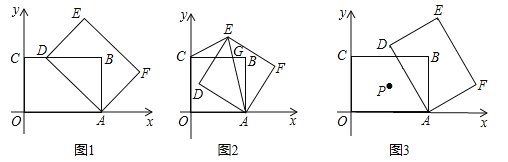
(1)如圖1,當點![]() 落在邊
落在邊![]() 上時,求
上時,求![]() 的長;
的長;
(2)如圖2,當![]() 時,矩形
時,矩形![]() 的對角線
的對角線![]() 交矩形
交矩形![]() 的邊
的邊![]() 于點
于點![]() ,連結
,連結![]() ,若
,若![]() 是等腰三角形,求直線
是等腰三角形,求直線![]() 的解析式.
的解析式.
(3)如圖3,當![]() 時,矩形
時,矩形![]() 的對稱中心為點
的對稱中心為點![]() .
.![]() 的面積為
的面積為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解同學們對網絡游戲的喜好和作業量多少的相關性,小明隨機對年級50名同學進行了調查,并將調查的情況進行了整理,如下表:
作業量多少 網絡游戲的喜好 | 認為作業多 | 認為作業不多 | 合計 |
喜歡網絡游戲 | 18 | 9 | 27 |
不喜歡網絡游戲 | 8 | 15 | 23 |
合計 | 26 | 24 | 50 |
如果小明再隨機采訪一名同學,那么這名同學是“喜歡網絡游戲并認為作業多”的可能性______“不喜歡網絡游戲并認為作業不多”的可能性.(填“>”,“=”或“<”)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為了解高二年級男生定點投籃的情況,隨機選取該校高二年級部分男生進行測試,每人投籃五次,以下是根據每人投中次數繪制的統計圖的一部分,
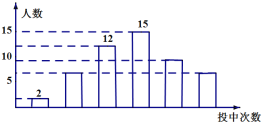
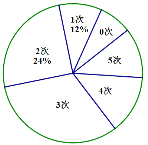
根據以上信息解答下列問題:
(1)被調查的男生中,投中次數為2次的有_____人,投中次數為1次的男生人數占被調查男生總數的百分比為_____%;
(2)被調查男生的總數為_____人,扇形統計圖中投中次數為3次的圓心角的度數為_____;
(3)若該校高二年級男生有200人,根據調查結果,估計該年級男生投中次數不少于3次的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,Rt△ABC中,∠ACB=90°,AC=5,BC=12,點D在邊AB上,以AD為直徑的⊙O,與邊BC有公共點E,則AD的最小值是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近一周,各個學校均在緊張有序地進行中考模擬考試,學生們通過模擬考試來調整自己的狀態并了解自己的學業水平.某中學物理教研組想通過此次中考模擬的成績來預估中考的各個分數段人數,在全年級隨機抽取了男.女各40名學生的成績(滿分為80分,女生成績中最低分為45分),并將數據進行整理分析,給出了下面部分信息:
①男生成績扇形統計圖和女生成績頻數分布直方圖如下:(數據分組為A組:x<50;B組:50≤x<60;C組:60≤x<70;D組:70≤x≤80)

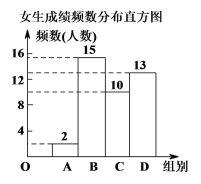
②男生C組中全部15名學生的成績為:
63,69,64,62,68,69,65,69,65,66,67,61,67,66,69.
③兩組數據的平均數.中位數.眾數.滿分率.極差(單位:分)如下表所示:
平均數 | 中位數 | 眾數 | 滿分率 | 極差 | |
男生 | 70 | b | c | 25% | 32 |
女生 | 70 | 68 | 78 | 15% | d |
(1)扇形統計圖A組學生中所對應的圓心角α的度數為 ,中位數b= ,眾數c= ,極差d= .
(2)通過以上的數據分析,你認為 (填“男生”或“女生”)的物理成績更好,并說明理由:
① ;② .
(3)若成績在70分(包含70分)以上為優秀,請你估計該校1200名學生中此次考試中優秀的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把三角形按如圖所示的規律拼圖案,其中第①個圖案中有4個三角形,第②個圖案中有6個三角形,第③個圖案中有8個三角形,…,按此規律排列下去,則第⑦個圖案中三角形的個數為( )
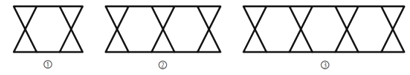
A. 12 B. 14 C. 16 D. 18
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,兩條射線BA//CD,PB和PC分別平分∠ABC和∠DCB,AD過點P,分別交AB,CD與點A,D.
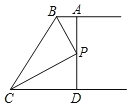
(1)求∠BPC的度數;
(2)若![]() ,求AB+CD的值;
,求AB+CD的值;
(3)若![]() 為a,
為a,![]() 為b,
為b,![]() 為c,求證:a+b=c.
為c,求證:a+b=c.
查看答案和解析>>
科目:初中數學 來源: 題型:
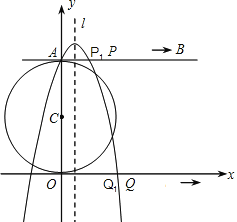
【題目】如圖,在平面直角坐標系中,以點C(0,4)為圓心,半徑為4的圓交y軸正半軸于點A,AB是⊙C的切線.動點P從點A開始沿AB方向以每秒1個單位長度的速度運動,點Q從O點開始沿x軸正方向以每秒4個單位長度的速度運動,且動點P、Q從點A和點O同時出發,設運動時間為t(秒).
(1)當t=1時,得到P1、Q1,求經過A、P1、Q1三點的拋物線解析式及對稱軸l;
(2)當t為何值時,直線PQ與⊙C相切?并寫出此時點P和點Q的坐標;
(3)在(2)的條件下,拋物線對稱軸l上存在一點N,使NP+NQ最小,求出點N的坐標并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com