
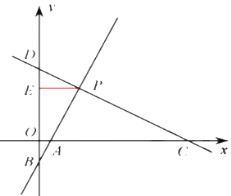
【題目】如圖,在直角坐標系內,已知![]() ,過點
,過點![]() 作互相垂直的兩條直線
作互相垂直的兩條直線![]() 、
、![]() ,
, ![]() 分別交
分別交![]() 軸于
軸于![]() 兩點;
兩點;![]() 分別交
分別交![]() 軸于
軸于![]() 兩點,已知
兩點,已知![]() .
.
(1)求![]() 的直線解析式;
的直線解析式;
(2)若點![]() 在
在![]() 軸的負半軸,已知拋物線
軸的負半軸,已知拋物線![]() 的對稱軸經過點
的對稱軸經過點![]() ,拋物線與
,拋物線與![]() 交于對稱軸左側的
交于對稱軸左側的![]() 點,當
點,當![]() 時,求拋物線的函數表達式.
時,求拋物線的函數表達式.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]()
【解析】
(1)過點![]() 作
作![]() 軸垂線,利用母子三角形的性質得到B的坐標,分情況建立圖形,利用相似三角形的性質求得A的坐標可得
軸垂線,利用母子三角形的性質得到B的坐標,分情況建立圖形,利用相似三角形的性質求得A的坐標可得![]() 的解析式.(2)先確定好
的解析式.(2)先確定好![]() 的解析式,利用
的解析式,利用![]() 求解
求解![]() 的解析式,確定點C的坐標,畫好符合題意的圖形,過M作對稱軸的垂線,找到轉化的相似三角形,確定好M的坐標,利用待定系數法求解解析式.
的解析式,確定點C的坐標,畫好符合題意的圖形,過M作對稱軸的垂線,找到轉化的相似三角形,確定好M的坐標,利用待定系數法求解解析式.
解:(1)過點![]() 作
作![]() 軸垂線,垂足為
軸垂線,垂足為![]() .
.![]() ,
,
![]() ,∴
,∴![]() ,設
,設![]() ,則
,則![]() ,
,
∴![]() ,解得
,解得![]() ,
,![]() ,
,
∴![]() 點坐標為
點坐標為![]() 或
或![]()
①當![]() 時,如圖1,
時,如圖1,![]() ,
,![]() ,因為
,因為![]() //
//![]() 軸,
軸,
所以![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
所以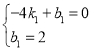 ,解得:
,解得: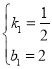 ,
,
所以![]() ;
;
②當![]() 時,如圖1,
時,如圖1,![]() ,
,![]() ,
,
同理:![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
同理:![]() ;
;
綜上所述,![]() 的直線解析式為
的直線解析式為![]() 或
或![]() .
.
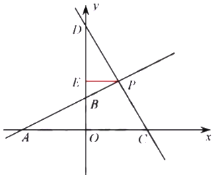
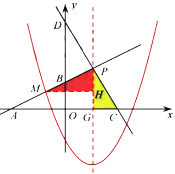
(2)當點![]() 在
在![]() 軸的負半軸時,
軸的負半軸時,![]() 的直線解析式為
的直線解析式為![]() ,因為
,因為![]() ,
,
所以![]() ,因為
,因為![]() ,所以
,所以![]()
設![]() ,把
,把![]() 代入解析式得,
代入解析式得,![]() ,
,
所以![]() ,所以
,所以![]() 點坐標為
點坐標為![]() .
.
對稱軸經過點![]() ,∴對稱軸
,∴對稱軸![]() 為直線
為直線![]() ,
,![]() 為對稱軸與
為對稱軸與![]() 軸的交點,
軸的交點,
∴設解析式為![]() ,
,![]() ,
,
∴作![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]()
所以![]() ,
,
∴![]() .
.
解得![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,代入拋物線
,代入拋物線![]()
求得解析式為![]() .
.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,⊙O的半徑為r(r>0).給出如下定義:若平面上一點P到圓心O的距離d,滿足![]() ,則稱點P為⊙O的“隨心點”.
,則稱點P為⊙O的“隨心點”.
(1)當⊙O的半徑r=2時,A(3,0),B(0,4),C(![]() ,2),D(
,2),D(![]() ,
,![]() )中,⊙O的“隨心點”是 ;
)中,⊙O的“隨心點”是 ;
(2)若點E(4,3)是⊙O的“隨心點”,求⊙O的半徑r的取值范圍;
(3)當⊙O的半徑r=2時,直線y=- x+b(b≠0)與x軸交于點M,與y軸交于點N,若線段MN上存在⊙O的“隨心點”,直接寫出b的取值范圍 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+3經過點A(﹣1,0)、B(3,0)兩點,且交y軸交于點C.
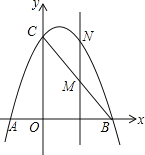
(1)求拋物線的解析式;
(2)點M是線段BC上的點(不與B、C重合),過M作MN∥y軸交拋物線于N,若點M的橫坐標為m,請用m的代數式表示MN的長;
(3)在(2)的條件下,連接NB,NC,是否存在點M,使△BNC的面積最大?若存在,求m的值;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖顯示了用計算機模擬隨機投擲一枚圖釘的某次實驗的結果.

下面有三個推斷:
①當投擲次數是500時,計算機記錄“釘尖向上”的次數是308,所以“釘尖向上”的概率是0.616;
②隨著實驗次數的增加,“釘尖向上”的頻率總在0.618附近擺動,顯示出一定的穩定性,可以估計“釘尖向上”的概率是0.618;
③若再次用計算機模擬實驗,則當投擲次數為1000時,“釘尖向上”的概率一定是0.620.
其中合理的是( )
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,直線y=x+4與拋物線y=﹣![]() x2+bx+c(b,c是常數)交于A、B兩點,點A在x軸上,點B在y軸上.設拋物線與x軸的另一個交點為點C.
x2+bx+c(b,c是常數)交于A、B兩點,點A在x軸上,點B在y軸上.設拋物線與x軸的另一個交點為點C.

(1)求該拋物線的解析式;
(2)P是拋物線上一動點(不與點A、B重合),
①如圖2,若點P在直線AB上方,連接OP交AB于點D,求![]() 的最大值;
的最大值;
②如圖3,若點P在x軸的上方,連接PC,以PC為邊作正方形CPEF,隨著點P的運動,正方形的大小、位置也隨之改變.當頂點E或F恰好落在y軸上,直接寫出對應的點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,AB=6,AD=9,∠BAD的平分線交BC于點E,交DC的延長線于點F,BG⊥AE于點G,BG=4![]() ,則△EFC的周長為( )
,則△EFC的周長為( )
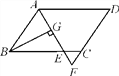
A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了提倡節約用電,某地區規定每月用電量不超過 a 千瓦·時,居民生活用電基本價格為每千瓦時 0.5 元;若每月用電量超過 a 千瓦·時,則超過部分按基本電價提高 20%收費.居住此地的老李家二月份用電 120 千瓦·時,所交的電費為 66 元.
(1)求 a 的值;
(2)老李登錄當地國家電網網絡平臺繳費后彈出一個對話框:您的家庭一月份和二月份的平均電費不超過0.54 元/千瓦·時,評為“節能小家庭”.試計算老李家一月份的用電量的范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校在商場購買甲、乙兩種不同足球,購買甲種足球共花費2000元,購買乙種足球共花費1400元,購買甲種足球數量是購買乙種足球數量的2倍,且購買一個乙種足球比購買一個甲種足球多花20元.
(1)求購買一個甲種足球、一個乙種足球各需多少元?
(2)為響應“足球進校園”的號召,這所學校決定再次購買甲、乙兩種足球共50個.恰逢該商場對兩種足球的售價進行調整,甲種足球售價比第一次購買時提高了10%,乙種足球售價比第一次購買時降低了10%,如果此次購買甲、乙兩種足球的總費用不超過2900元,那么這所學校最多可購買多少個乙種足球?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在下列函數圖象上任取不同兩點P(x1,y1),Q(x2,y2),一定能使(x2﹣x1)(y2﹣y1)>0成立的是( )
A.y=﹣2x+1(x<0)B.y=﹣x2﹣2x+8(x<0)
C.y=![]() (x>0)D.y=2x2+x﹣6(x>0)
(x>0)D.y=2x2+x﹣6(x>0)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com