
【題目】如圖,在菱形ABCD中,過對角線BD上任意一點P,作EF∥BC,GH∥AB,下列結論:①圖中共有3個菱形;②△BEP≌△BGP;③四邊形AEPH的面積等于△ABD的面積的一半;④四邊形AEPH的周長等于四邊形GPFC的周長.其中正確的是________.(填序號)

【答案】①②④
【解析】∵圖中有三個菱形,如菱形ABCD、菱形HOFD、菱形BEPG,∴①正確;
∵四邊形ABCD是菱形,
∴AB∥DC,AD∥BC,∠ABD=∠CBD,
∵EF∥BC,GH∥AB,
∴四邊形BEPG是平行四邊形,
∴PE=BG,PG=BE,
在△BEP和△PGB中,
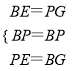
∴△BEP≌△PGB(SSS),
∴②正確;
∵只有當H為AD中點,E為AB中點時,四邊形AEPH的面積等于△ABD的面積的一半,∴③錯誤;
∵四邊形ABCD是菱形,
∴AB∥CD,AD∥BC,
∵EF∥BC,GH∥AB,
∴AD∥EF∥BC,AB∥GH∥CD,
∴四邊形AEPH、四邊形HPFD、四邊形BEPG、四邊形PFCG是平行四邊形,
∴AH=BG=PE,AE=HP=DF,BE=PG=CF,DH=PF=VG,
∵四邊形ABCD是菱形,
∴∠EBP=∠GBP,
∵PE∥BG,
∴∠EPB=∠GBP,
∴∠EBP=∠EPB,
∴BE=PE,
∴AH=PE=BG=BE=CF=PG,
同理AE=HP=DF=PF=CG,
∴四邊形AEPH的周長=四邊形GPFC的周長,∴④正確;
故答案為:①②④.


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,將一張長方形紙片分別沿著EP,FP對折,使B落在B′,C落在C′.
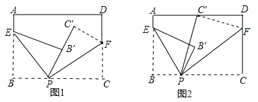
(1)若點P,B′,C′在同一直線上(圖1),求兩條折痕的夾角∠EPF的度數;
(2)若點P,B′,C′不在同一直線上(圖2),且∠B′PC′=10°,求∠EPF的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,AC與BD相交于點O,E是OD的中點,連接AE并延長交DC于點F,則DF:FC=( ) 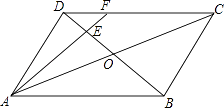
A.1:4
B.1:3
C.1:2
D.1:1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD,點F為正方形ABCD內一點,△BFC逆時針旋轉后能與△BEA重合.
(1)旋轉中心是點 ,旋轉角度為 度;
(2)判斷△BEF的形狀為 ;
(3)若∠BFC=90°,說明AE∥BF.

查看答案和解析>>
科目:初中數學 來源: 題型:
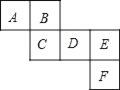
【題目】如圖所示是一個正方體的表面展開圖,請回答下列問題:
(1)與面B,C相對的面分別是 ;
(2)若A=a3+![]() a2b+3,B=﹣
a2b+3,B=﹣![]() a2b+a3,C=a3﹣1,D=﹣
a2b+a3,C=a3﹣1,D=﹣![]() (a2b+15),且相對兩個面所表示的代數式的和都相等,求E,F分別代表的代數式.
(a2b+15),且相對兩個面所表示的代數式的和都相等,求E,F分別代表的代數式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】.如圖 1,AB∥CD,直線 EF 交 AB 于點 E,交 CD 于點 F,點 G 在 CD 上,點 P在直線 EF 左側,且在直線 AB 和 CD 之間,連接 PE,PG.
(1) 求證: ∠EPG=∠AEP+∠PGC;
(2) 連接 EG,若 EG 平分∠PEF,∠AEP+ ∠ PGE=110°,∠PGC=![]() ∠EFC,求∠AEP 的度數.
∠EFC,求∠AEP 的度數.
(3) 如圖 2,若 EF 平分∠PEB,∠PGC 的平分線所在的直線與 EF 相交于點 H,則∠EPG 與∠EHG之間的數量關系為 .
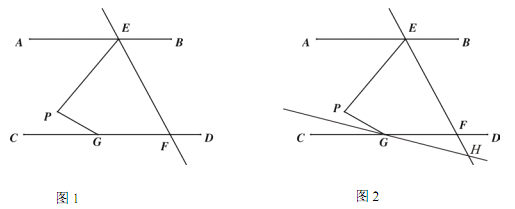
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現在,蘇寧商場進行促銷活動,出售一種優惠購物卡(注:此卡只作為購物優惠憑證不能頂替貨款),花300元買這種卡后,憑卡可在這家商場按標價的8折購物.
(1)顧客購買多少元金額的商品時,買卡與不買卡花錢相等?在什么情況下購物合算?
(2)小張要買一臺標價為3500元的冰箱,如何購買合算?小張能節省多少元錢?
(3)小張按合算的方案,把這臺冰箱買下,如果商場還能盈利25%,這臺冰箱的進價是多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com