
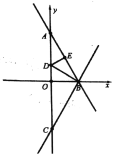
【題目】如圖,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,點
,點![]() 為線段
為線段![]() 的中點,
的中點,![]() 的平分線
的平分線![]() 與
與![]() 軸相較于點
軸相較于點![]() ,
,![]() 、
、![]() 兩點關于
兩點關于![]() 軸對稱.
軸對稱.

(1)一動點![]() 從點
從點![]() 出發(fā),沿適當的路徑運動到直線
出發(fā),沿適當的路徑運動到直線![]() 上的點
上的點![]() ,再沿適當的路徑運動到點
,再沿適當的路徑運動到點![]() 處.當
處.當![]() 的運動路徑最短時,求此時點
的運動路徑最短時,求此時點![]() 的坐標及點
的坐標及點![]() 所走最短路徑的長.
所走最短路徑的長.
(2)點![]() 沿直線
沿直線![]() 水平向右運動得點
水平向右運動得點![]() ,平面內是否存在點
,平面內是否存在點![]() 使得以
使得以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形為菱形,若存在,請直接寫出點
為頂點的四邊形為菱形,若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)點![]() 的坐標為
的坐標為![]() ,點
,點![]() 所走最短路徑的長為
所走最短路徑的長為![]() ;(2)存在,點
;(2)存在,點![]() 的坐標為
的坐標為![]() 或
或![]() .
.
【解析】
(1)先根據直線的解析式求出點A、B的坐標,再根據直角三角形和角平分線以及對稱的性質得出點C、D、E的坐標,然后利用待定系數法可求出直線BC的解析式,最后根據對稱性質確定最短路徑,求出直線![]() 的解析式,聯(lián)立兩個函數的解析式即可得;
的解析式,聯(lián)立兩個函數的解析式即可得;
(2)根據菱形的性質,分兩種情況:BD為邊和BD為對角線,然后分別利用菱形的性質、兩點之間的距離公式列出等式求解即可.
(1)對于![]()
當![]() 時,
時,![]() ,解得
,解得![]() ,則點B的坐標為
,則點B的坐標為![]()
當![]() 時,
時,![]() ,則點A的坐標為
,則點A的坐標為![]()
![]() 點
點![]() 為線段
為線段![]() 的中點
的中點
![]()
由點A、B的坐標得:![]()
在![]() 中,
中,![]() ,即
,即![]()
![]()
![]() 平分
平分![]()
![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
![]()
![]()
![]()
![]() 、
、![]() 兩點關于
兩點關于![]() 軸對稱
軸對稱
![]()
設直線BC的解析式為![]()
將點![]() 代入得
代入得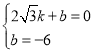 ,解得
,解得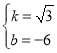
則直線BC的解析式為![]()
如圖,作點D關于直線BC的對稱點![]() ,連接ED交BC于點F
,連接ED交BC于點F
由對稱的性質、兩點之間線段最短可知,點P所走最短路徑的長為![]() 的長
的長
由對稱的性質可知,![]()
過點![]() 作
作![]() 軸于點G
軸于點G
在![]() 和
和![]() 中,
中,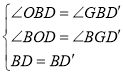
![]()
![]()
![]()
![]()
由兩點之間的距離公式得:![]()
設直線![]() 的解析式為
的解析式為![]()
將點![]() 代入得
代入得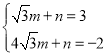 ,解得
,解得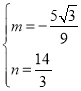
則直線![]() 的解析式為
的解析式為![]()
聯(lián)立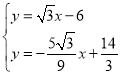 ,解得
,解得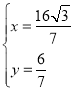
則點![]() 的坐標為
的坐標為![]() ;
;
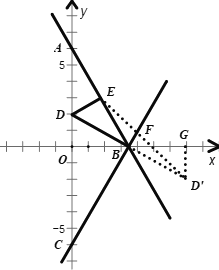
(2)存在,點![]() 的坐標的求解過程如下:
的坐標的求解過程如下:
![]() ,點
,點![]() 沿直線
沿直線![]() 水平向右運動得點
水平向右運動得點![]()
![]() 可設點
可設點![]() 的坐標為
的坐標為![]() ,且
,且![]()
由菱形的性質,分以下兩種情況:
①若BD為邊
由菱形的定義得:![]()
由兩點之間的距離公式得:![]()
解得![]() 或
或![]() (舍去)
(舍去)
則點![]() 的坐標為
的坐標為![]()
②若BD為對角線
由菱形的定義得:![]()
由兩點之間的距離公式得:![]()
解得![]()
則點![]() 的坐標為
的坐標為![]()
綜上,點![]() 的坐標為
的坐標為![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】某汽車銷售公司一位銷售經理1—5月份的汽車銷售統(tǒng)計圖如下:
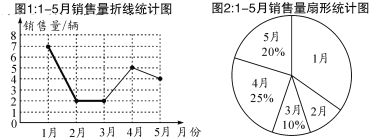
(1)已知1月的銷售量是2月的銷售量的3.5倍,則1月的銷售量為________輛,在扇形圖中,2月的銷售量所對應的扇形的圓心角大小為________;
(2)補全圖中銷售量折線統(tǒng)計圖;
(3)已知4月份銷售的車中有3輛國產車和2輛合資車,國產車分別用G1,G2,G3表示,合資車分別用H1,H2表示,現(xiàn)從這5輛車中隨機抽取兩輛車參加公司的回饋活動,請用列舉法(畫樹狀圖或列表)求出“抽到的兩輛車都是國產車”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解放碑某商場地下停車場有5個出入口,每天早晨7點開始對外停車且此時車位空置率為80%,在每個出入口的車輛數均是勻速出入的情況下,如果開放2個進口和3個出口,7小時車庫恰好停滿:如果開放3個進口和2個出口,4小時車庫恰好停滿.2019年清明節(jié)期間,由于商場人數增多,早晨7點時的車位空置率變?yōu)?/span>60%,又因為車庫改造,只能開放2個進口和1個出口,則從早晨7點開始經過_______小時車庫恰好停滿.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形紙片ABCD中,AD=5,AB=3.若M為射線AD上的一個動點,將△ABM沿BM折疊得到△NBM.若△NBC是直角三角形.則所有符合條件的M點所對應的AM長度的和為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
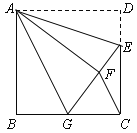
【題目】如圖,正方形ABCD中,AB=6,點E在邊CD上,且CD=3DE.將△ADE沿AE對折至△AFE,延長EF交邊BC于點G,連結AG、CF.
(1)求證:①△ABG≌△AFG; ②BG=GC;
(2)求△FGC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線y4x4與x軸,y軸分別交于點A,B,點A在拋物線yax2bx3a(a0)上,將點B向右平移3個單位長度,得到點C.
(1)拋物線的頂點坐標為 (用含a的代數式表示)
(2)若a1,當t-1≤x≤t時,函數yax2bx3a(a0)的最大值為y1,最小值為y2,且y1y22,求t的值;
(3)若拋物線與線段BC恰有一個公共點,結合函數圖象,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線C1:y=a(x+2)2-5的頂點為P,與x軸相交于A、B兩點(點A在點B的左邊),點B的橫坐標是1.
(1) 求P點坐標及a的值;
(2)如圖(1),
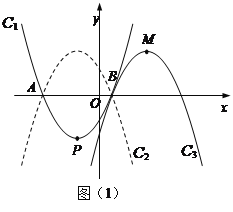
拋物線C2與拋物線C1關于x軸對稱,將拋物線C2向右平移,平移后的拋物線記為C3,C3的頂點為M,當點P、M關于點B成中心對稱時,求C3的解析式;
(3) 如圖(2),
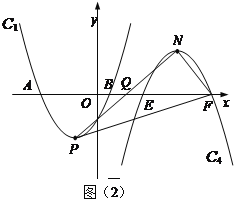
點Q是x軸正半軸上一點,將拋物線C1繞點Q旋轉180°后得到拋物線C4.拋物線C4的頂點為N,與x軸相交于E、F兩點(點E在點F的左邊),當以點P、N、F為頂點的三角形是直角三角形時,求點Q的坐標.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com