【題目】如圖，將矩形ABCD沿對角線BD折疊，點C落在點E處，BE交AD于點F，已知∠BDC=62°，則∠DFE的度數為（ ）
A. 31° B. 28° C. 62° D. 56°
科目：初中數學 來源： 題型：
【題目】已知二次函數y=x2﹣2x﹣1．
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
（1）請在表內的空格中填入適當的數；
（2）根據列表，請在所給的平面直角坐標系中畫出y=x2﹣2x﹣1的圖象；
（3）當x在什么范圍內時，y隨x增大而減小；
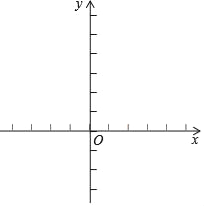
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料，并回答問題.事實上，在任何一個直角三角形中，兩條直角邊的平方之和一定等于斜邊的平方，這個結論就是著名的勾股定理.請利用這個結論，完成下面活動:
一個直角三角形的兩條直角邊分別為
，那么這個直角三角形斜邊長為____；
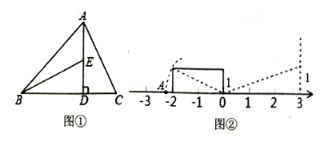
如圖①，
于
，求
的長度；
如圖②，點
在數軸上表示的數是____請用類似的方法在圖2數軸上畫出表示數
的
點(保留痕跡).
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖
，點
將線段
分成兩部分，如果
，那么稱點為線段的黃金分割點．
某研究小組在進行課題學習時，類似地給出“黃金分割線”的定義：直線
將一個面積為
的圖形分成兩部分，這兩部分的面積分別為
，
，如果
，那么稱直線為該圖形的黃金分割線．（如圖
）
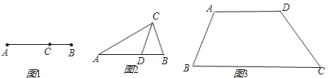
問題．試在圖
的梯形中畫出至少五條黃金分割線，并說明理由．
類似“黃金分割線”得“黃金分割面”定義：截面
將一個體積為
的圖形分成體積為V1
、
的兩個圖形，且
，則稱直線為該圖形的黃金分割面．
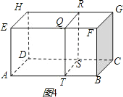
問題：如圖
，長方體
中，
是線段上的黃金分割點，證明經過點且平行于平面
的截面
是長方體的黃金分割面．
查看答案和解析>>
科目：初中數學 來源： 題型：
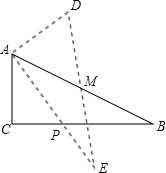
【題目】如圖，在△ABC中，∠C=90°，AB=10，cosB=
，點M是AB邊的中點，將△ABC繞著點M旋轉，使點C與點A重合，點A與點D重合，點B與點E重合，得到△DEA，且AE交CB于點P，那么線段CP的長是__________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知，在平面直角坐標系中，點
，
，過
點作直線
與
軸互相垂直，
為軸上的一個動點，且
.
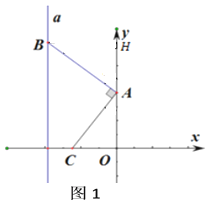
（1）如圖1，若點是第二象限內的一個點，且
時，求點的坐標；（用
的代數式表示）
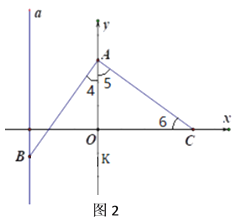
（2）如圖2，若點是第三象限內的一個點，設點的坐標
，求的取值范圍：
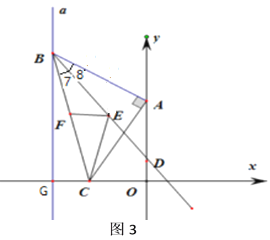
（3）如圖3，連接
，作
的平分線
，點
、
分別是射線與邊上的兩個動點，連接
、
，當
時，試求
的最小值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我國古代數學著作《九章算術》中的一個問題．原文是：今有池方一丈，葭生其中央，出水尺．引葭赴岸，適與岸齊問水深、葭長各幾何譯文大意是：如圖，有一個水池，水面是一個邊長為10尺的正方形，在水池正中央有一根蘆葦，它高出水面1尺．如果把這根蘆葦拉向水池邊的中點，它的頂端恰好到達池邊的水面．問水的深度與這根蘆葦的長度分別是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠C=90°，∠B=30°，以A為圓心，任意長為半徑畫弧分別交AB、AC于點M和N，再分別以M、N為圓心，大于MN的長為半徑畫弧，兩弧交于點P，連結AP并延長交BC于點D，則下列說法中正確的個數是
①AD是∠BAC的平分線；②∠ADC=60°；③點D在AB的中垂線上；④S△DAC：S△ABC=1：3．
A．1 B．2 C．3 D．4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
