
【題目】如圖,![]() 是
是![]() 的直徑,
的直徑,![]() .
.
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)若點![]() 是
是![]() 的中點,連接
的中點,連接![]() 交
交![]() 于點
于點![]() ,當
,當![]() ,
,![]() 時,求
時,求![]() 的值.
的值.

【答案】(1)見解析;(2)![]()
【解析】
(1)證明△ADC∽△BAC,可得∠BAC=∠ADC=900,從而可判斷AC是⊙O的切線;
(2)根據(1)所得△ADC∽△BAC,可得出CA的長度,從而判斷∠CFA=∠CAF,利用等腰三角形的性質得出AF的長度,繼而得出DF的長,在Rt△AFD中利用勾股定理可得出AF的長.
(1)∵AB是⊙O的直徑,
∴∠ADB=∠ADC=90°,
∵∠B=∠CAD,∠C=∠C,
∴△ADC∽△BAC,
∴∠BAC=∠ADC=90°,
∴BA⊥AC,
∴AC是⊙O的切線.
(2)∵BD=5,CD=4,
∴BC=9,
∵△ADC∽△BAC(已證),
∴![]() ,即AC2=BC×CD=36,
,即AC2=BC×CD=36,
解得:AC=6,
在Rt△ACD中,AD= ![]() ,
,
∵∠CAF=∠CAD+∠DAE=∠ABF+∠BAE=∠AFD,
∴CA=CF=6,
∴DF=CA-CD=2,
在Rt△AFD中,AF= ![]() .
.


 53隨堂測系列答案
53隨堂測系列答案科目:初中數學 來源: 題型:
【題目】(2017重慶A卷第11題)如圖,小王在長江邊某瞭望臺D處,測得江面上的漁船A的俯角為40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡長BC=10米,則此時AB的長約為( )(參考數據:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
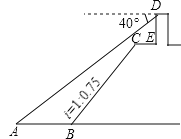
A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠ABC ∠ACB ,BD 、CD 分別平分△ABC 的內角 ∠ABC 、外角 ∠ACP ,BE平分外角 ∠MBC 交 DC 的延長線于點 E ,以下結論:①∠BDE ![]() ∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正確的結論有( )
∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正確的結論有( )
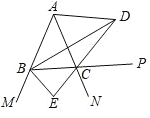
A.1 個B.2 個C.3 個D.4 個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知命題“等腰三角形兩腰上的高線長相等”
(1)請寫出該命題的逆命題;
(2)判斷(1)中命題的真假,并畫出圖形,補充已知,求證,及證明過程.
圖形:
已知:在△ABC中,CD⊥AB,BE⊥AC,且______.
求證:______.
證明:
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料并把解答過程補充完整.
問題:在關于x,y的二元一次方程組![]() 中,x>1,y<0,求a的取值范圍.
中,x>1,y<0,求a的取值范圍.
在關于x,y的二元一次方程組中,利用參數a的代數式表示x,y,然后根據x>1,y<0列出關于參數a的不等式組即可求得a的取值范圍.
解:由![]() ,解得
,解得 ,又因為x>1,y<0,所以
,又因為x>1,y<0,所以 ,解得________.
,解得________.
請你按照上述方法,完成下列問題:
已知x-y=4,x>3,y<1,求x+y的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠BAC=30°,AM是∠BAC的平分線,過M作ME∥BA交AC于E,作MD⊥BA,垂足為D,ME=10cm,則MD=_________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A、B、C在數軸上分別表示的數為-10,2,8,點D是BC中點,點E是AD中點.
(1)求EB的長;
(2)若動點P從點A出發,以1cm/s的速度向點C運動,達到點C停止運動,點Q從點C出發,以2cm/s的速度向點A運動,到達點A停止運動,若運動時間為ts,當t為何值時,PQ=3cm?
(3)點A,B,C開始在數軸上運動,若點A以1cm/s的速度向左運動,同時,點B和點C分別以4cm/s和9cm/s的速度向右運動,假設t秒鐘過后,若點B與點C之間的距離表示為BC,點A與點B之間的距離表示為AB,請問:AB-BC的值是否隨時間t的變化而變化?若變化,請說明理由;若不變,請求其常數值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了豐富同學們的課余生活,某學校將舉行“親近大自然”戶外活動.現隨機抽取了部分學生進行主題為“你最想去的景點是”的問卷調查,要求學生只能從“A(世博園),B(勞動公園),C(月牙島公園),D(赫圖阿拉城)”四個景點中選擇一項,根據調查結果,繪制了如下兩幅不完整的統計圖:

(1)本次共調查了多少名學生?
(2)補全條形統計圖;
(3)在扇形統計圖中,求B(勞動公園)部分所占的圓心角度數;
(4)若該學校共有3600名學生,試估計該校最想去月牙島公園的學生人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com