Question

【題目】如圖，正比例函數的圖象與反比例函數的圖象交于A、B兩點，過點A作AC垂直x軸于點C，連結BC．若△ABC的面積為2．

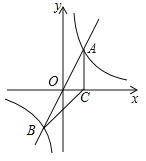
（1）求k的值；

（2）x軸上是否存在一點D，使△ABD為直角三角形？若存在，求出點D的坐標；若不存在，請說明理由．

Answer 1

【答案】（1）k=2；（2）D（5，0）或（﹣5，0）或（，0）或D（，0）．

【解析】試題分析：（1）首先根據反比例函數與正比例函數的圖象特征，可知A、B兩點關于原點對稱，則O為線段AB的中點，故△BOC的面積等于△AOC的面積，都等于1，然后由反比例函數的比例系數k的幾何意義，可知△AOC的面積等于，從而求出k的值；

（2）先將與聯立成方程組，求出A、B兩點的坐標，然后分三種情況討論：①當AD⊥AB時，求出直線AD的關系式，令y=0，即可確定D點的坐標；②當BD⊥AB時，求出直線BD的關系式，令y=0，即可確定D點的坐標；③當AD⊥BD時，由O為線段AB的中點，可得OD=AB=OA，然后利用勾股定理求出OA的值，即可求出D點的坐標．

試題解析：（1）∵反比例函數與正比例函數的圖象相交于A、B兩點，∴A、B兩點關于原點對稱，∴OA=OB，∴△BOC的面積=△AOC的面積=2÷2=1，又∵A是反比例函數圖象上的點，且AC⊥x軸于點C，∴△AOC的面積=，∴，∵k＞0，∴k=2．故這個反比例函數的解析式為；

（2）x軸上存在一點D，使△ABD為直角三角形．將與聯立成方程組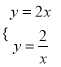得： ，解得： ， ，∴A（1，2），B（﹣1，﹣2），

①當AD⊥AB時，如圖1，

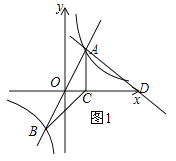
設直線AD的關系式為，將A（1，2）代入上式得： ，∴直線AD的關系式為，令y=0得：x=5，∴D（5，0）；

②當BD⊥AB時，如圖2，

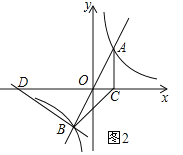
設直線BD的關系式為，將B（﹣1，﹣2）代入上式得： ，∴直線AD的關系式為，令y=0得：x=﹣5，∴D（﹣5，0）；

③當AD⊥BD時，如圖3，

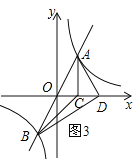
∵O為線段AB的中點，∴OD=AB=OA，∵A（1，2），∴OC=1，AC=2，由勾股定理得：OA==，∴OD=，∴D（，0），

根據對稱性，當D為直角頂點，且D在x軸負半軸時，D（，0）；

故x軸上存在一點D，使△ABD為直角三角形，點D的坐標為（5，0）或（﹣5，0）或（，0）或D（，0）．